树的遍历
在计算机科学里,树的遍历(也称为树的搜索)是图的遍历的一种,指的是按照某种规则、不重复地访问某种树的所有结点的过程。具体的访问操作可能是检查结点的值、更新结点的值等。不同的遍历方式,其访问结点的顺序是不一样的。以下虽然描述的是二叉树的遍历算法,但它们也适用于其他树形结构。
结点(Node)
javascript 中结点的定义:
function TreeNode(val) {
this.val = val;
this.left = this.right = null;
}
深度优先遍历(Depth-first traversal)
先访问根结点,后选择一子结点访问并访问该结点的子结点,持续深入后直到找到叶子结点为止,然后回溯到前一个结点,访问该结点的其他子结点,直到遍历完所有可达结点为止。可以用递归或栈的方式实现深度优先遍历。
二叉树的遍历有三种,前序遍历、中序遍历和后序遍历。其中,前、中、后序,表示的是结点与它的左右子树结点遍历打印的先后顺序。
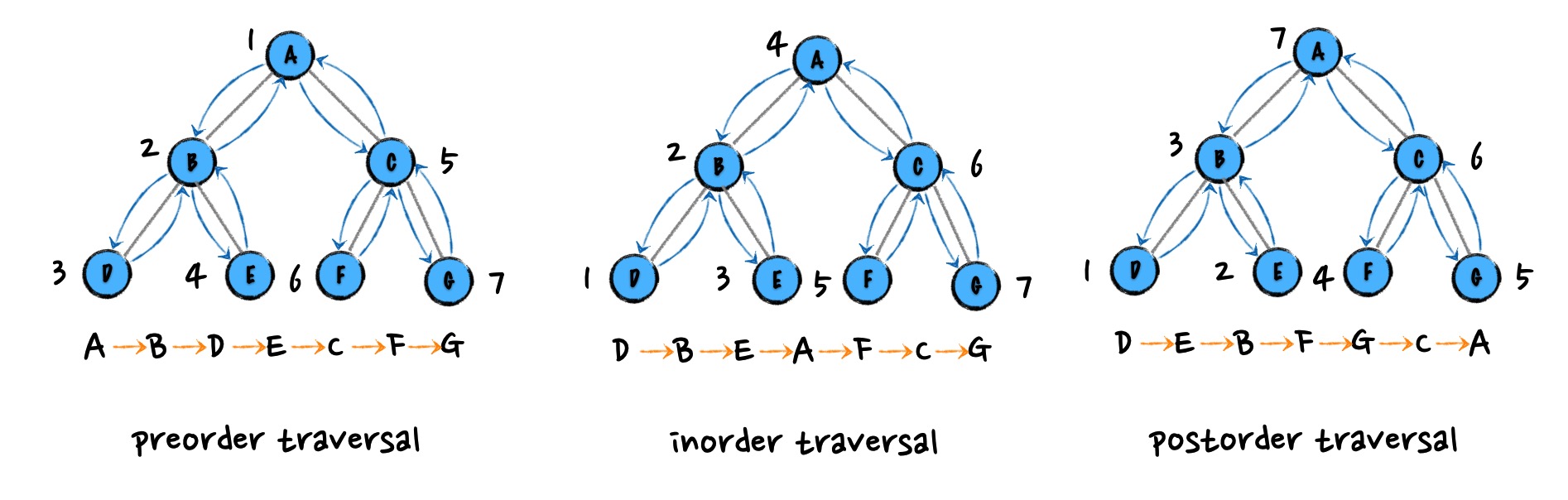
前序遍历(preorder traversal)
前序遍历是指,对于树中的任意结点来说,先打印这个结点,然后再打印它的左子树,最后打印它的右子树。
- 递归
/**
* @param {TreeNode} root
* @return {number[]}
*/
let preorderTraversal = function (root) {
return root
? [
root.val,
...preorderTraversal(root.left),
...preorderTraversal(root.right)
]
: [];
};
- 时间复杂度:O(n)。递归函数 T(n) = 2 * T(n/2) + 1 = 2 * (2 * T(n/4) + 1) + 1 = 2 ^ logn + 2^(logn-1) + ... + 2 + 1 ~= n
- 空间复杂度:最坏情况下需要空间 O(n),平均情况为 O(logn)
- 迭代
/**
* @param {TreeNode} root
* @return {number[]}
*/
let preorderTraversal = function (root) {
if (!root) return [];
let arr = [root]; // 使用数组模拟栈,存储待处理的结点,先放右结点,后放左结点
let result = [];
let temp;
while (arr.length > 0) {
temp = arr.pop();
result.push(temp.val);
temp.right && arr.push(temp.right);
temp.left && arr.push(temp.left);
}
return result;
};
- 时间复杂度:访问每个结点恰好一次,时间复杂度为 O(n)
- 空间复杂度:取决于树的结构,最坏情况存储整棵树,因此空间复杂度是 O(n)
中序遍历(inorder traversal)
中序遍历是指,对于树中的任意结点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
- 递归
/**
* @param {TreeNode} root
* @return {number[]}
*/
let inorderTraversal = function (root) {
return root
? [
...inorderTraversal(root.left),
root.val,
...inorderTraversal(root.right)
]
: [];
};
- 时间复杂度:O(n)。递归函数 T(n) = 2 * T(n/2) + 1 = 2 * (2 * T(n/4) + 1) + 1 = 2 ^ logn + 2^(logn-1) + ... + 2 + 1 ~= n
- 空间复杂度:最坏情况下需要空间 O(n),平均情况为 O(logn)
数据量大的时候,使用递归会占用大量的内存,因此更建议在数据规模不大的时候使用。
为什么数据量大的时候,递归效率低?
- 函数调用开销大,递归中需要调用多次函数,就需要建立许多的访问链和控制链,以及函数内局部变量和调用时传递的参数等都需要申请空间
- 递归中会进行频繁的入栈出栈操作,而且递归层数达到一定的值,还可能出现内存溢出的情况
递归的优势是什么?
- 代码更加简洁清晰,更易于理解和使用
- 对于实现难度很高的算法,使用递归将大大减少工作量
- 迭代
/**
* @param {TreeNode} root
* @return {number[]}
*/
let inorderTraversal = function (root) {
if (!root) {
return [];
}
let result = [];
let stack = []; // 存储待处理的结点
let current = root;
while (current || stack.length > 0) {
while (current) {
stack.push(current);
current = current.left;
// 不断把左子树push进栈中,直到叶子结点
}
current = stack.pop(); // 从栈的末尾取一个元素
// 经过前面的while循环,此时栈中保存的就是所有的左结点和根结点。栈中所有的元素的左子树已经经过了处理(push进了栈中),取当前元素的val push到结果中
result.push(current.val);
current = current.right; // 对当前元素的右子树重复上述过程
}
return result;
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
后序遍历(postorder traversal)
后序遍历是指,对于树中的任意结点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个结点本身。
- 递归
/**
* @param {TreeNode} root
* @return {number[]}
*/
let postorderTraversal = function (root) {
return root
? postorderTraversal(root.left)
.concat(postorderTraversal(root.right))
.concat(root.val)
: [];
};
- 时间复杂度:O(n)。递归函数 T(n) = 2 * T(n/2) + 1 = 2 * (2 * T(n/4) + 1) + 1 = 2 ^ logn + 2^(logn-1) + ... + 2 + 1 ~= n
- 空间复杂度:最坏情况下需要空间 O(n),平均情况为 O(logn)
- 迭代
/**
* @param {TreeNode} root
* @return {number[]}
*/
let postorderTraversal = function (root) {
let result = [];
let current;
let stack = [root]; // 栈中存储待处理的结点
while (stack.length) {
current = stack.pop();
result.unshift(current.val); // 注意此处使用unshift方法,每次都从头部插入,则插入顺序为中-右-左
current.left && stack.push(current.left);
current.right && stack.push(current.right);
}
return result;
};
二叉树的前序遍历是:中-左-右,而二叉树的后序遍历顺序是:左-右-中,因此可以参考前序遍历,先处理中间结点,再分别处理右、左结点。
广度优先遍历(Breadth-first traversal)
二叉树的层次遍历
/**
* @param {TreeNode} root
* @return {number[][]}
*/
let levelOrder = function (root) {
let queue = [root]; // 使用队列,先进先出
let p = root;
let ans = [];
while (queue.length) {
p = queue.shift();
ans.push(p.val);
p.left && queue.push(p.left);
p.right && queue.push(p.right);
}
return ans;
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
N 叉树的层次遍历
/**
* @param {Node} root
* @return {number[][]}
*/
let levelOrder = function (root) {
if (!root) return [];
let ans = [];
let queue = [root];
let level = 0;
while (queue.length) {
ans[level] = [];
let queueLen = queue.length; // 存储当前待处理队列的长度,也即当前层次待处理的结点数目
while (queueLen) {
let node = queue.shift();
ans[level].push(node.val);
node.children && queue.push(...node.children);
queueLen--;
}
level++;
}
return ans;
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
二叉树的垂直遍历
对位于 (X, Y) 的每个结点而言,其左右子结点分别位于 (X-1, Y-1) 和 (X+1, Y-1)。把一条垂线从 X = -infinity 移动到 X = +infinity ,每当该垂线与结点接触时,按从上到下的顺序报告结点的值( Y 坐标递减)。如果两个结点位置相同,则首先报告的结点值较小。按 X 坐标顺序返回非空报告的列表。每个报告都有一个结点值列表。
思路:
- 以 X 坐标为 key,以相同 X 坐标的结点及其 Y 坐标集合而成的数组为 value,生成对象 object
- 取所有的 X 坐标并排序,对 X 坐标相同的结点,按照 Y 坐标排序,若 X 与 Y 都相同时 按 val 排序
/**
* @param {TreeNode} root
* @return {number[][]}
*/
let verticalTraversal = function (root) {
let obj = {};
// 存储待处理的结点
let arr = [{node: root, x: 0, y: 0}];
while (arr.length > 0) {
let mynode = arr.shift();
let node = mynode.node;
let x = mynode.x;
let y = mynode.y;
// 以X轴坐标为 key,对结点分组
if (obj[x] === undefined) {
obj[x] = [{val: node.val, y: y}];
} else {
obj[x].push({val: node.val, y: y});
}
node.left !== null && arr.push({node: node.left, x: x - 1, y: y - 1});
node.right !== null && arr.push({node: node.right, x: x + 1, y: y - 1});
}
let res = [];
// 存储 升序的 x 坐标值
let sortedXArr = Object.keys(obj).sort((a, b) => a - b);
for (let i = 0; i < sortedXArr.length; i++) {
// 针对X坐标相同的结点,再根据 Y 坐标从大到小排列
let temp = [];
obj[sortedXArr[i]].sort(function (a, b) {
if (b.y === a.y) return a.val - b.val;
return b.y - a.y;
});
obj[sortedXArr[i]].forEach(function (x) {
temp.push(x.val);
});
res.push(temp);
}
return res;
};
- 时间复杂度:O(nlogn)
- 空间复杂度:O(n)