Skip to main content

树的基本概念

定义 (Definition)​

在计算机科学中，树 是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由 n（n>0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

  1. 每个节点都只有有限个子节点或无子节点；
  2. 没有父节点的节点称为根节；
  3. 每一个非根节点有且只有一个父节点；
  4. 除了根节点外，每个子节点可以分为多个不相交的子树；
  5. 树里面没有环路；

看几个例子:

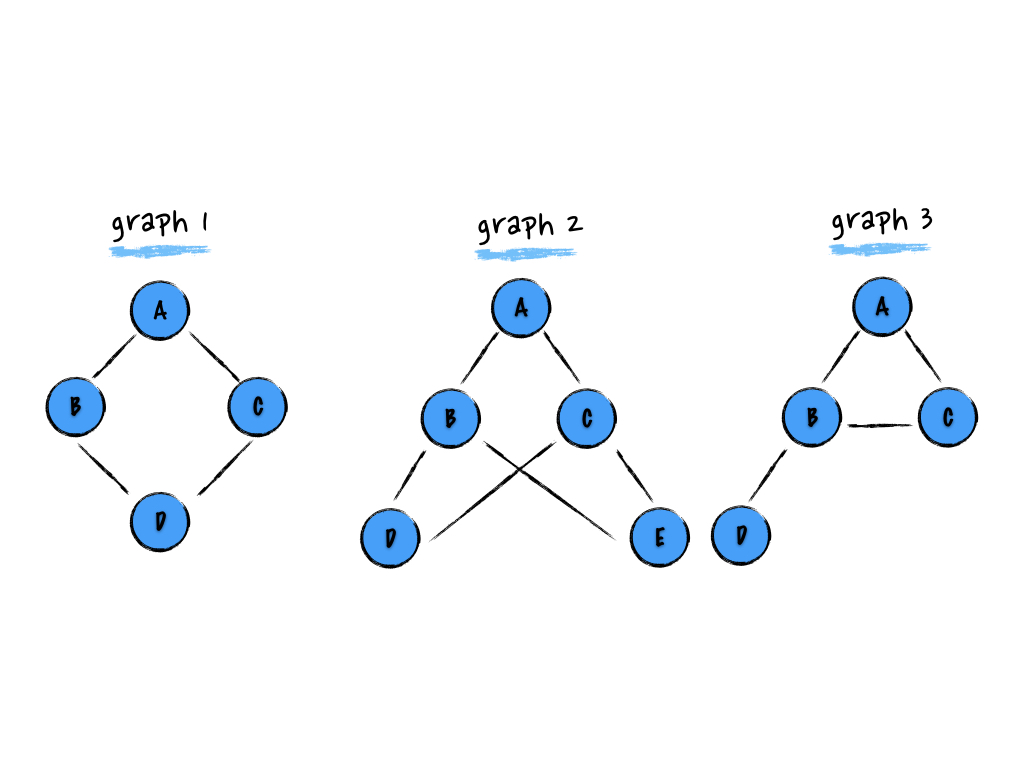
tree-traversal

图 1

上图中的结构均不是树。

分析：

  • graph 1：

    • 违背了特点 3：每个非根节点有且只有一个根节点。根据特点 2 我们知道没有父节点的节点为根节点，如果把节点 A 当做根节点，那么其他节点为非根节点，对于非根节点 D，它有两个父节点 B 和 C。同理，如果把节点 D 当做根节点，那么 A 节点有两个父节点，不符合特点 3。
    • 违背了特点 5：graph 1 的树里面出现了环 A - B - D - C - A。

  • graph 2：

    • 违背了特点 3：如果把节点 A 当做根节点，那么对于非根节点 D，它有两个父节点 B 和 C，对于非根节点 E，它有两个父节点 B 和 C。
    • 违背了特点 4：除了根节点外，每个子节点可以分为多个不相交的子树。节点 A 的左子树和右子树相交了。
    • 违背了特点 5：树里面出现了环 A - B - D - C - A 和 A - B - E - C - A。

  • graph 3：

    • 违背了特点 5：树里面出现了环 A - B - C - A。
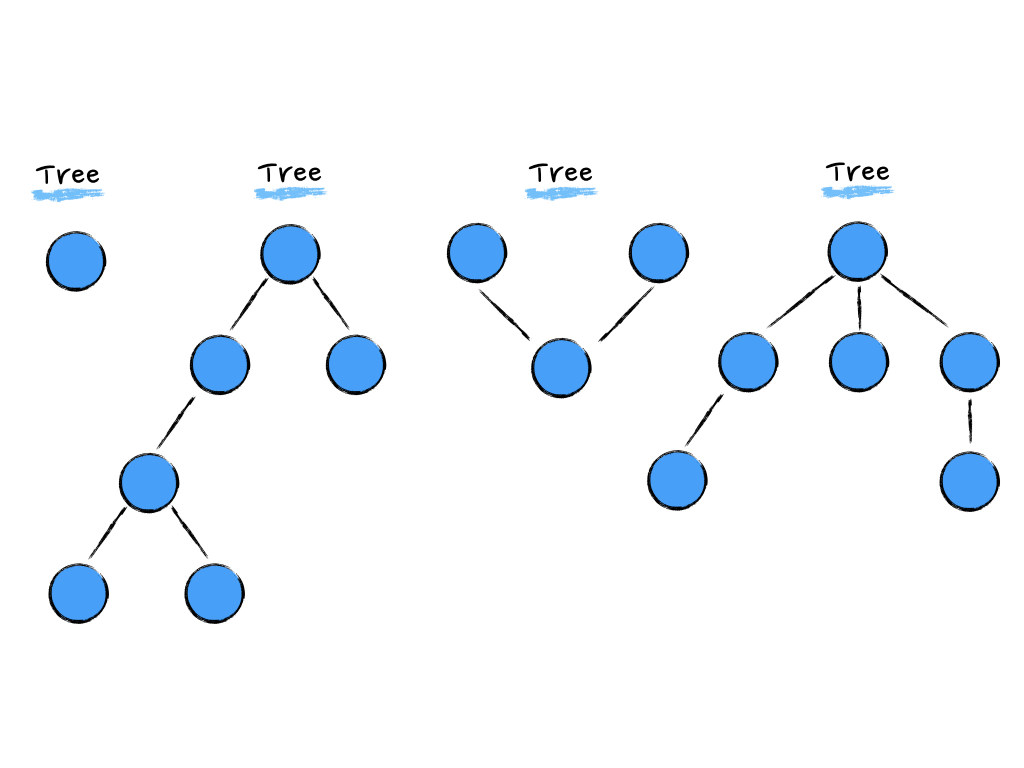
tree-traversal

图 2

上图中的结构都是树，可以对照 5 个特点进行验证。

通过上面几个例子可以看出 树 这种数据结构很像现实中的“树”，上图 树 中的每个圆圈就是树的一个 节点，圆圈之间的相连的线表示了节点之间的关系，通常上下相连我们称为“父子节点”，有相同直接父节点的我们称为“兄弟节点”，这和现实中的“辈分”也是很相似的，对应的还可以有“祖父节点”等。比如在下图中：A 节点就是 B 节点的父节点，B 节点就是 A 节点的子节点。F 和 G 两个节点的父节点是同一个节点，所以他们互为兄弟节点，同理，H、I、J 也互为兄弟节点。而 A 节点是没有父节点的，把这样的节点叫做根节点，根节点只有一个。F、G、K、I 和 L 是没有子节点的，这样的节点我们叫做叶子节点或者叶节点。

tree-traversal

图 3

高度 (Height)​

对于任意节点 n，n 的高度为从 n 到叶节点的最长路径长，所有树叶的高度为 0。以上图图 3 为例，节点 A 的高度为 4，节点 A 到叶子节点的最长路径可以是 A - C - E - H - K，也可以是 A - C - E - J - L，两个路径的长都为 4，也就是路径上的“边”数为 4。同理可知，节点 D 的高度为 1，节点 F 的高度为零。

caution

节点 A 的高度不是 5，高度指的是路径长，也就是最长路径上的“边”数，而不是路径上的“节点”数。

树的高度 (Height of tree)​

根节点到叶节点的最长路径长。以上图图 3 为例，节点 A 为根节点，其高度为 4，则树的高度为 4。

深度 (Depth)​

对于任意节点 n，n 的深度为从根到 n 的唯一路径长，根的深度为 0。以上图图 3 为例，节点 D 的高度为 2，节点 D 到根点的唯一路径为 D - B - A，路径的长为 2，所以 D 的深度为 2。同理可知节点 K 的深度为 4。

层 (Level)​

对于任意节点 n，n 的层数为 n 的深度 + 1。以上图图 3 为例，节点 D 的深度为 2，则其所在层为 3，也就是节点 D 到根点的唯一路径为 D - B - A 上的“节点”数。同理可知节点 K 所在的层数为 5。

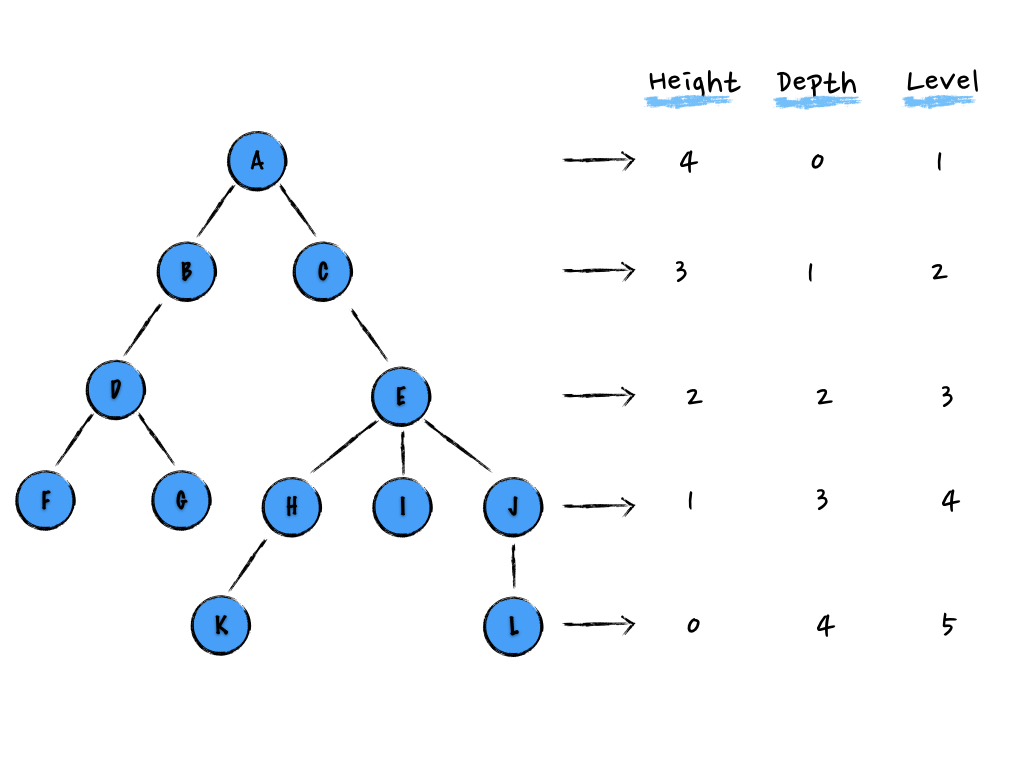
tree-traversal

图 4

对比 高度 深度 层 这三个概念，我们可以类比生活中的含义来简化记忆：

  • 高度: 在我们生活中，高度其实就是从下往上度量，比如某位同学高度为 178cm，就是从下、从地面向上量。类比树，任意节点的高度也是从下、从最底层开始度量，这里的最底层就是树的叶节点。
  • 深度: 而深度就是从上往下度量，比如水中鱼的深度就是从地面向下度量。类比树，任意节点的深度也是从上、从最顶层开始度量，这里的最顶层就是树的根节点。
  • 层: 层数和深度类似，只不过深度算的是最长路径上的“边”数，而层数的算的是“节点”数。

度 (Degree)​

对于任意节点 n，n 含有的子树的个数称为节点 n 的度。以上图图 3 为例，节点 D 有两个子树，则节点 D 的度为 2。同理可知节点 E 所在的层数为 3，节点 H 的度为 1，节点 K 的度为 0。

树的度 (Degree of tree)​

一棵树中，最大的节点度称为树的度。以上图图 3 为例，度最大的节点是 D，其的度为 3，则树的度为 3。

参考资料​

  1. 数据结构与算法之美, by 王争
  2. 树 (数据结构), wikipedia