二叉树的基本概念
定义 (Definition)
在计算机科学中,二叉树 (Binary tree) 是每个节点最多只有两个分支(即不存在分支度大于 2 的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。

图 1
上图这些都是二叉树,都满足任意节点的度 <= 2 的特性。
与普通树不同,普通树的节点个数至少为 1,而二叉树的节点个数可以为 0;普通树节点的最大分支度没有限制,而二叉树节点的最大分支度为 2;普通树的节点无左、右次序之分,而二叉树的节点有左、右次序之分。
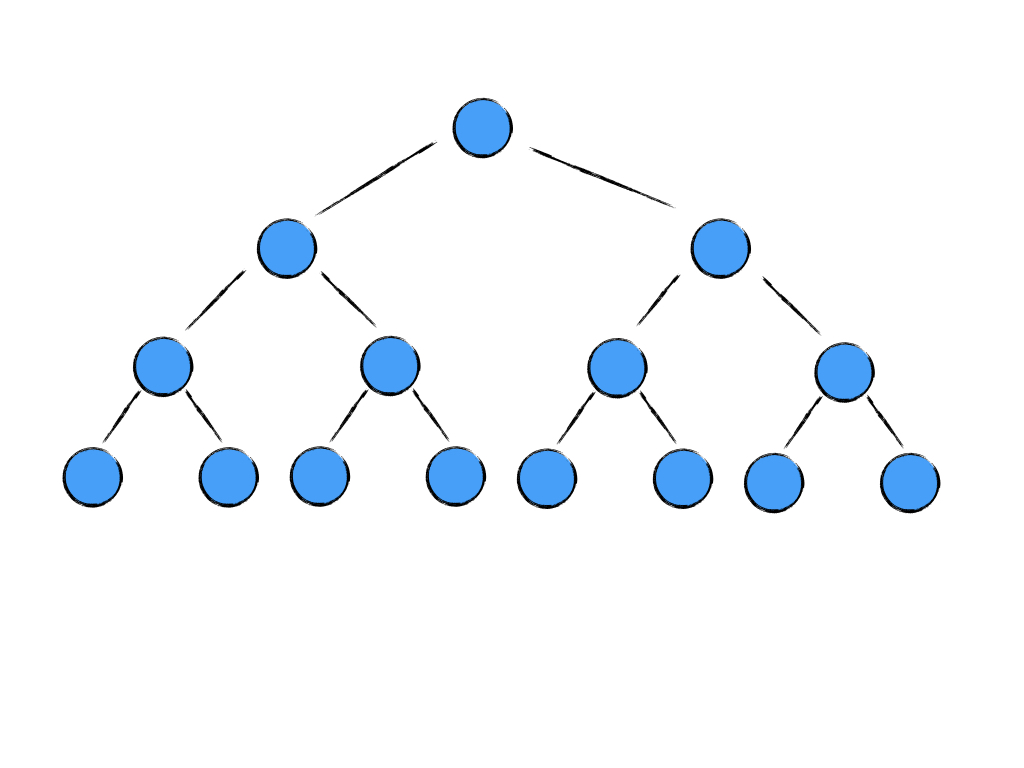
图 2
有两个比较关键的数字可以稍微看下:
- 二叉树的第 i 层至多拥有 2i-1个节点。推导:二叉树每个节点最多有 2 个子节点。“最多”就是把节点全填满,那么:
- 第一层是 20 = 1 个
- 第二层是第一层的每个节点再“生”两个子节点,就是 (20) * 2 = 21 = 2 个
- 第三层是第二层的每个节点再“生”两个子节点,就是 (21) * 2 = 22 = 4 个
- 第四层是第三层的每个节点再“生”两个子节点,就是 (22) * 2 = 23 = 8 个
- ...以此类推...
- 第 i 层是第 i-1 层的每个节点再“生”两个子节点,就是 (2i-2) * 2 = 2i-1 个
- 层数为 i 的二叉树至多总共有 2i -1 个节点(如果按照深度 k 算就是 2k+1 -1,因为深度计算的是“边数”,层数 i = 深度 k + 1,下同)。推导:“最多”就是把节点全填满,层数为 i 的树的总节点数就是上面每层都填满的节点数相加:20 + 21 + ... + 2i-1 = 2i -1。
求和推算:20 + 21 + ... + 2i-1 是等比数列,还记得等比数列求和公式吗:Sn = a1(1-qn)/(1-q)。这里 a1 就是 1,q 就是 2, n 是项的个数就是 i (指数从 0 到 i-1 一共有 i 项),所以 Si = 1*(1-2i)/(1-2) = 2i-1。
TLNR:有的同学可能会好奇等比数列公式推算过程:设 s = a1q0 + a1q1 + ... + a1qi-1,等号两遍都乘以 q 得:qs = a1q1 + a1q2 + ... + a1qi,两式相减得:(q-1)s = a1qi - a1q0 = a1(qi-q0) = a1(qi-1),所以 s=a1(qi-1)/(q-1)==a1(1-qi)/(1-q)。
满二叉树 (Perfect Binary Tree)
一棵层数为 i,且有 2i -1 个节点的二叉树,称为满二叉树又叫做完美二叉树。这种树的特点是每一层上的节点数都是最大节点数。除了叶节点外,每个节点都有左右两个孩子。像上图图 2就是一个满二叉树。
满二叉树的一些性质:对于一棵层数为 i 的满二叉树
- 共有 2i-1 个结点
- 结点个数一定为奇数(因为别人都是成双成对的,但是根节点是自己)
- 第 i 层有 2i-1 个结点
- 有 2i-1 个叶子
通过上面的分析这些性质都不难理解,不再赘述。
完全二叉树 (Complete Binary Tree)
在一颗二叉树中,若除最后一层外的其余层都是满的,并且最后一层要么是满的,要么在右边缺少连续若干节点,则此二叉树为完全二叉树(Complete Binary Tree)。
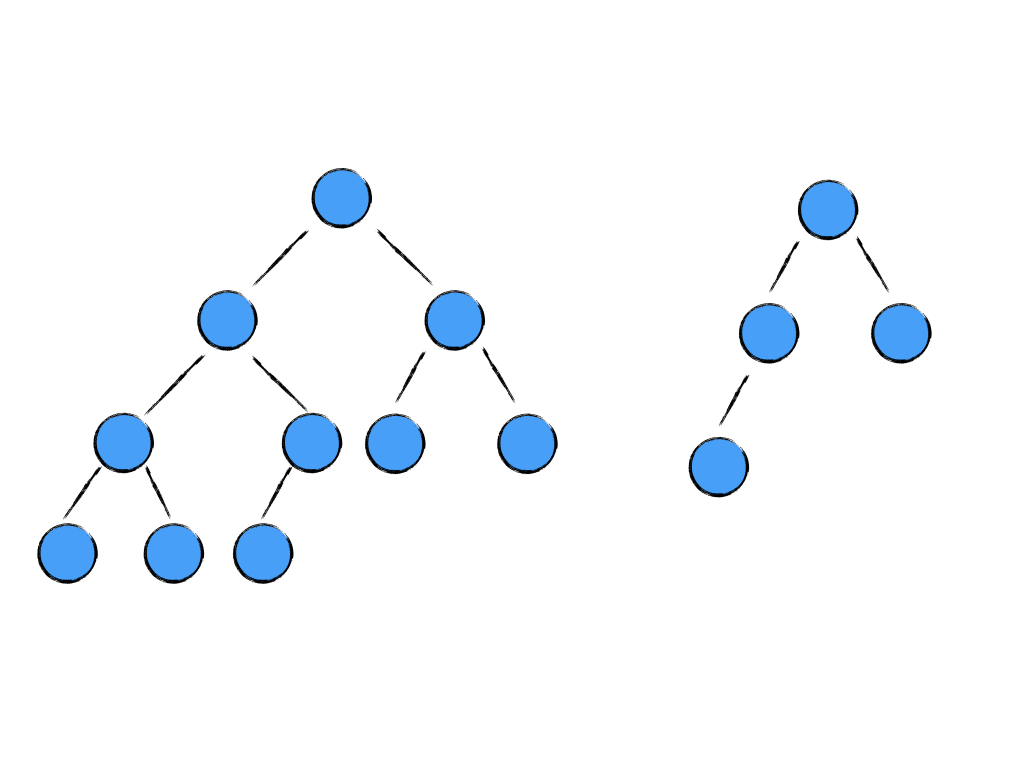
图 3
像上图图 2和图 3这样的树都是完全二叉树。他们要么最后一层是满的,要么最后一层的节点都靠左站,只缺右边的节点。
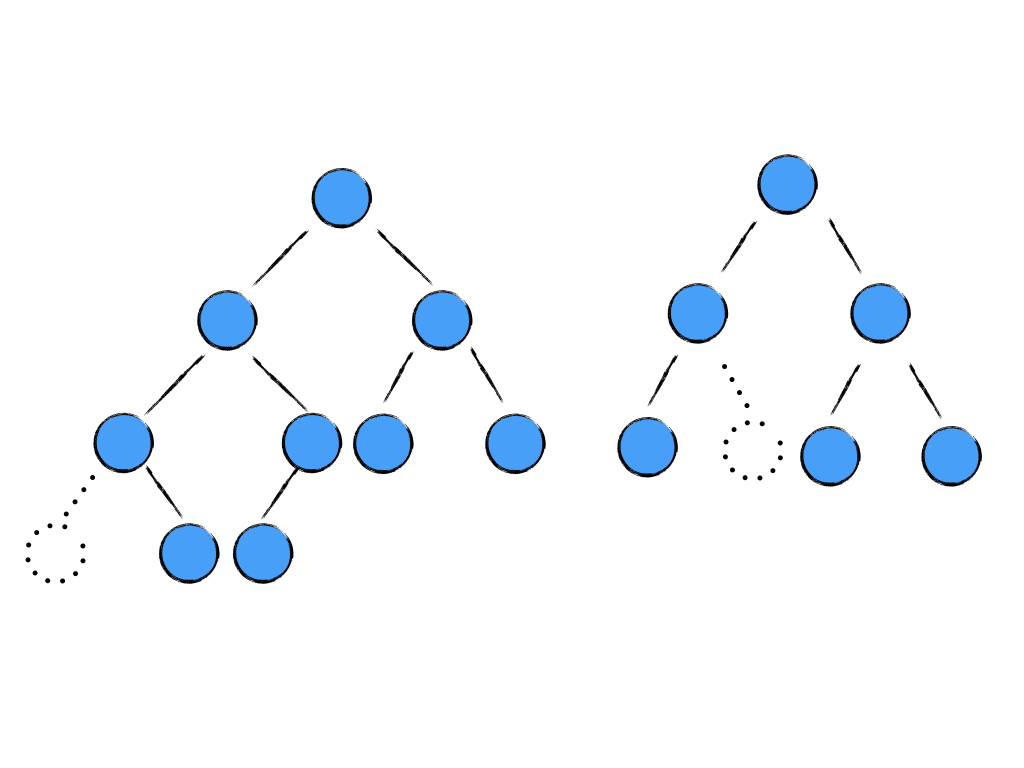
图 4
像上图图 4这样的树就不是完全二叉树。它们缺少的节点用虚线表示,可以清晰的分辨出来。
完全二叉树的一些性质:
- 具有 n 个节点的完全二叉树的深度为 ⌊ log2 n ⌋ +1。以下图为例,一个深度 k 为 3 (层数 i 为 4) 的树,最少拥有 8 个节点,再少一个就少了一层,最多拥有 15 个节点。深度 k = ⌊ log2 n ⌋,层数 i = ⌊ log2 n ⌋ + 1。这里要注意深度是“边数”,深度 = 层数 - 1。简单做下分析:

图 5
- 最少:除了最后一层外是满二叉树,最后一层只有 1 个节点。红框中的满二叉树的节点总数为 2k-1 = 2i-1-1(k 为二叉树的深度),则最少的情况就是这个情况下加 1 个节点,数量是:(2k-1)+1 = 2k,也等于 (2i-1-1)+1 = 2i-1(i 为二叉树的总层数),可以看出此时 k = ⌊ log2 n ⌋,i = ⌊ log2 n ⌋ + 1。
- 最多:除了最后一层外是满二叉树,最后一层也满了。上面已知满二叉树的节点总数的 2k+1-1 = 2i-1,可以看出此时也有 k = ⌊ log2 n ⌋,i = ⌊ log2 n ⌋ + 1。
向下取整其实就抹平了最后一层的个数差异了。
- 深度为 k 、层数为 i 的完全二叉树,至少有 2k = 2i-1 个节点,至多有 2k+1 -1,也就是 2i -1 个节点。这个从性质 1 的推理过程中可以看出,不再赘述。
满二叉树和完全二叉树对比 (Compare)
| 完全二叉树 | 满二叉树 | |
|---|---|---|
| 总结点数 n | 2c-1 <= n <= 2c -1 | n = 2c -1 |
| 树的层数 c | c = ⌊ log2 n ⌋ + 1 | c = log2n+1 |
存储结构 (Storage Structure)
二叉树的存储结构有两种:顺序存储和链式存储。
顺序存储 (Sequential Storage)
顺序存储就是用数组保存,但并不是任意的树都适合用数组。像满二叉树和完全二叉树就可以使用数组来存储,因为它们使用数组能做到紧凑排列而不浪费空间。原因如下:
如果我们把根节点放到数组 index = 0 的位置,那么,对于某个索引为 i 的节点,它的左子索引就是 2 i + 1,它的右子索引就是 2 i + 2,它的父节点索引为 ⌊ (i - 1) / 2 ⌋。
如果我们把根节点放到数组 index = 1 的位置,那么,对于某个索引为 i 的节点,它的左子索引就是 2 i,它的右子索引就是 2 i + 1,它的父节点索引为 ⌊ i / 2 ⌋。
举例如下:
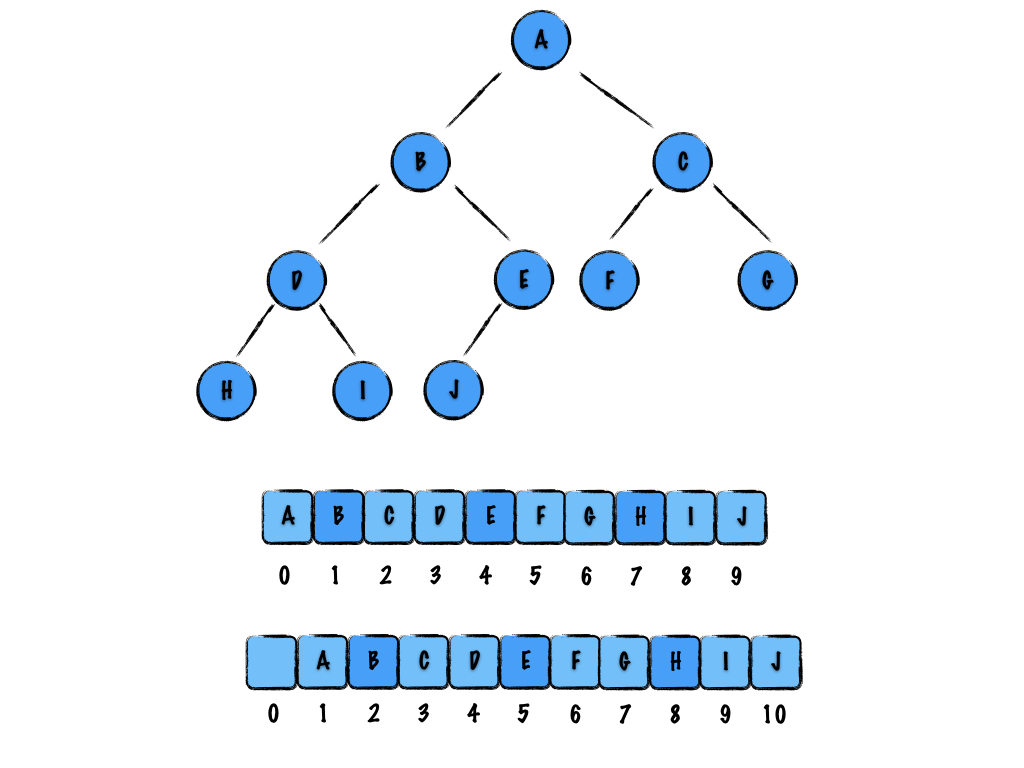
图 6
这些不需要死记硬背,用到的时候以根节点为例子,看下左右节点的索引就可以得出规律了。顺序存储的好处是我们可以快速的定位某个节点的左右子节点,甚至父节点。
但是如果是一颗比较随意的树使用数组来存储,为了确定左右子和父节点的索引关系,就要产生很多空余的空间,造成浪费,如下图。所以一般只有满二叉树和完全二叉树蚕蛹顺序存储方式,更加一般的树结构我们往往使用链式存储。
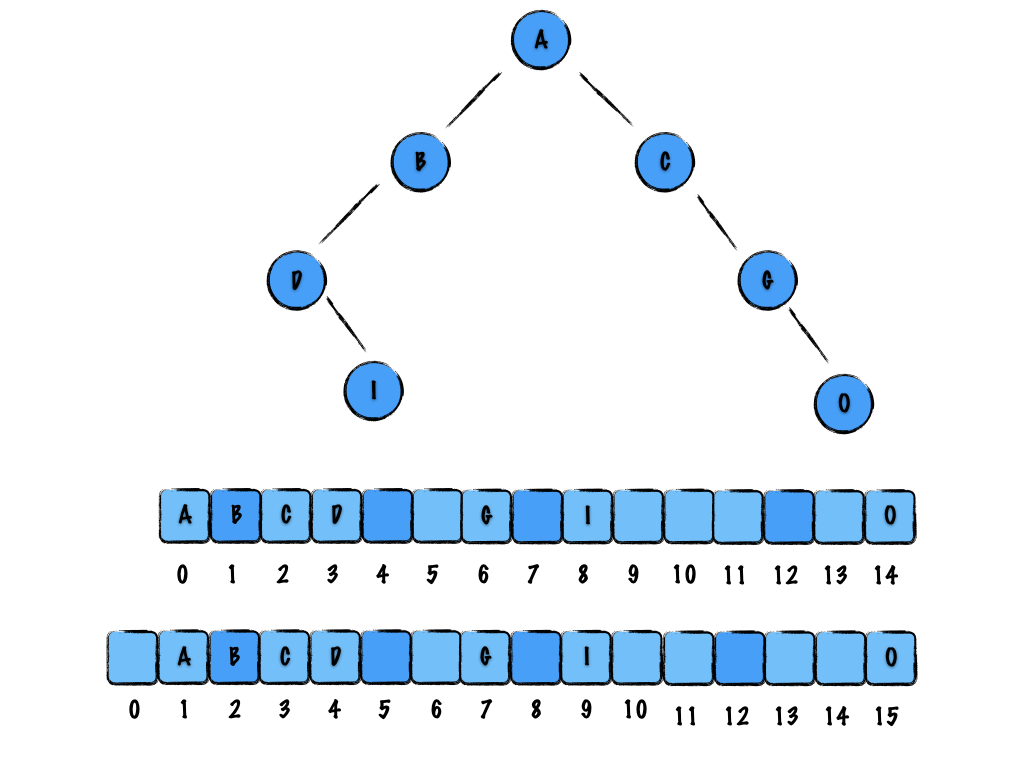
图 7
链式存储 (Chain Storage)
链式存储是基于指针或者引用的,把给每个数据节点加上两个指针指向它的左右子节点,如下图:
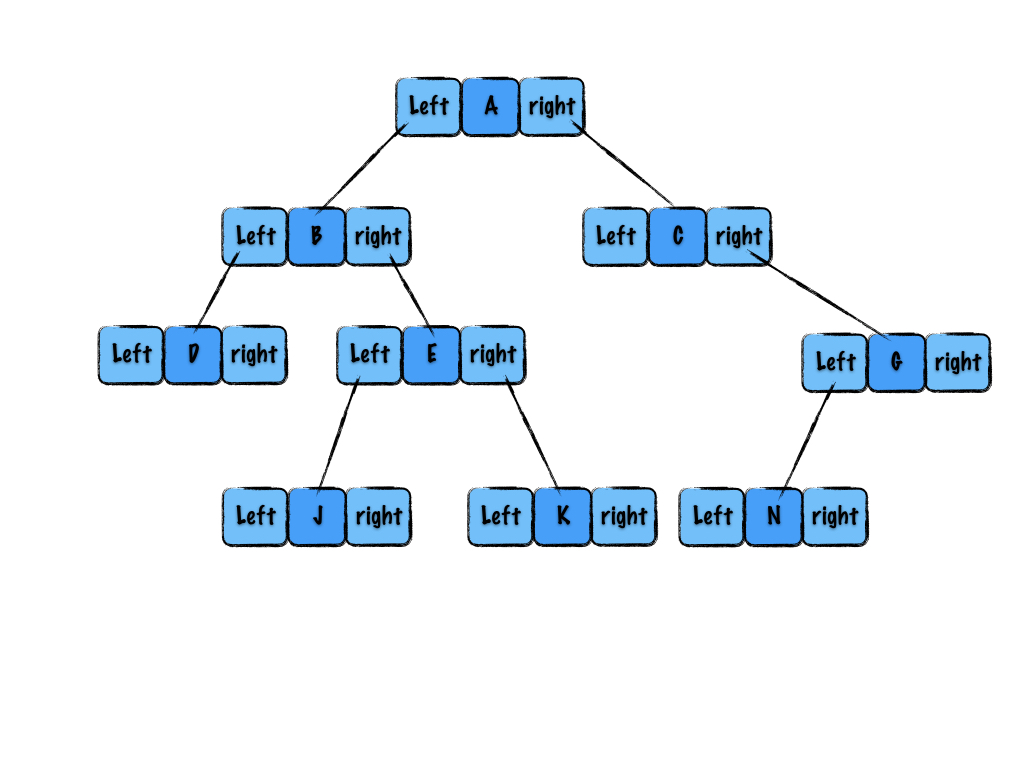
图 8
那些没有指向别的节点的 left 和 right 指针均指向 null。
通过上面的分析可以看出,链式存储可以减少一般数在顺序存储时空间的浪费,但是相比于顺序存储,顺序能:1.快速的获取父节点,2.根据计算出的索引能单独的访问任意节点。这是非常大的便利,但是一般的链式存储就做不到这两点了。对于第一点,链式存储可以通过在数据节点上再额外加父节点的指针来做,但是这样数据结构和对树的操作就会相对变得复杂很多,对于第二点,链式存储就无能为力了,如果想访问到某一个节点,就只能从根节点开始逐个向下遍历,直到到达目标节点。