Skip to main content

数组基本介绍

数组简介​

首先来简单了解一下线性表（Linear List），它是数据按照一定的线性顺序排列而成的数据集合。所谓线性和非线性只在逻辑层面上讨论，而不考虑实际存储。线性表中除了头部和尾部元素外（头部元素有后继元素，尾部元素有前驱元素），其他元素都同时有前驱和后继元素。数组(Array)就是一种线性表数据结构，它用一组连续的内存空间，来存储一组元素。常见的线性表结构还有链表(Linked list)、队列(Queue)、栈(Stack)等。

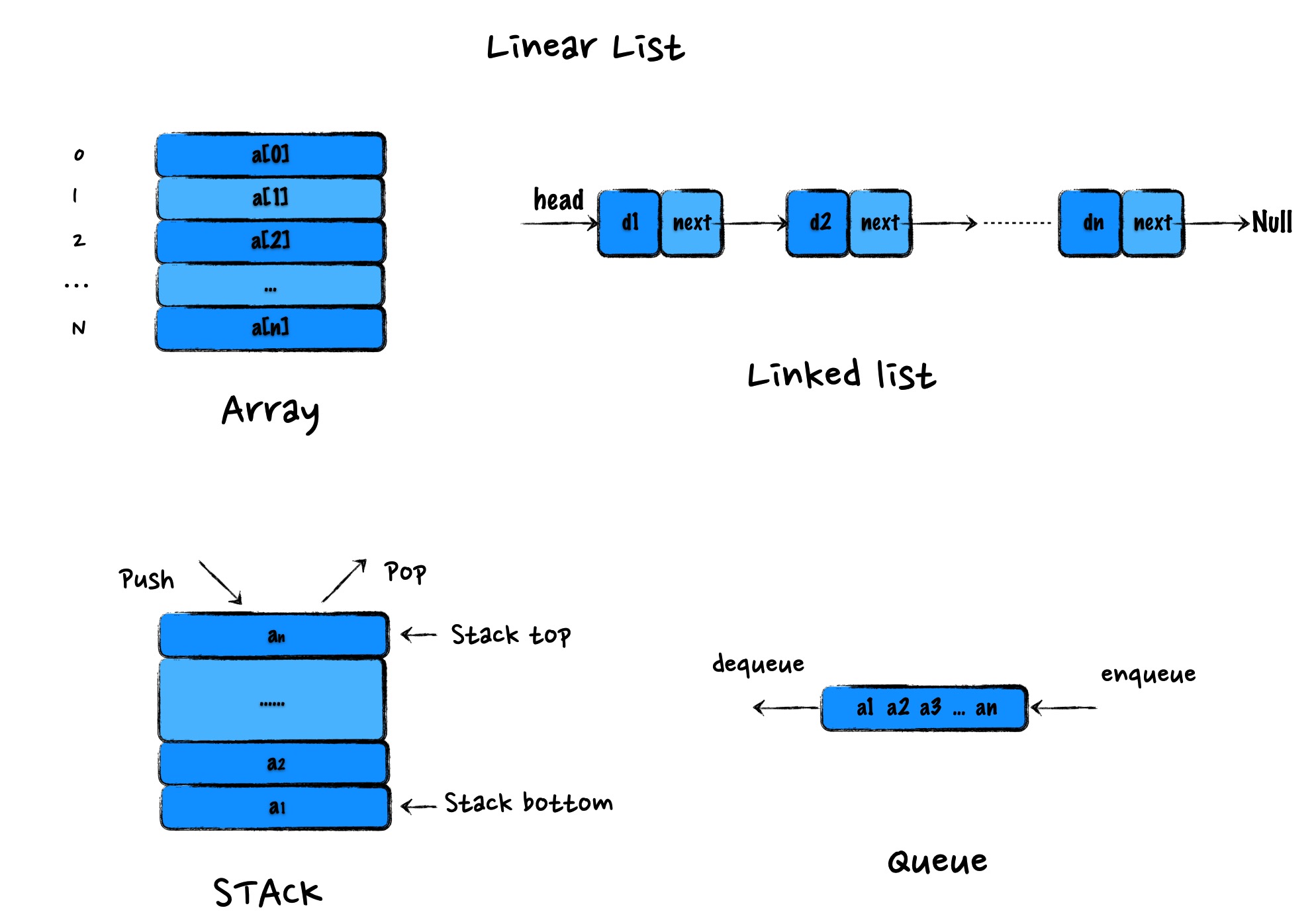
linearList
tip

数组中存储的元素都是相同数据类型吗？

在具体的编程语言中，数组的实现方式具有一定差别。比如 C++ 和 Java 中，数组中的元素类型必须保持一致，而 Python 和 Javascript 中则可以不同。Python 中的数组叫做 list，具有更多的高级功能。

数组的索引（index）​

数组通过名为 索引 的数字来标识每个元素在数组中的位置，且在大多数编程语言中，索引是从 0 算起的。可以通过索引快速访问数组中的元素，时间复杂度为 O(1)。索引是数组特有的，而线性表是没有的，这是它与数组最大的不同点。

数组的操作​

读取元素​

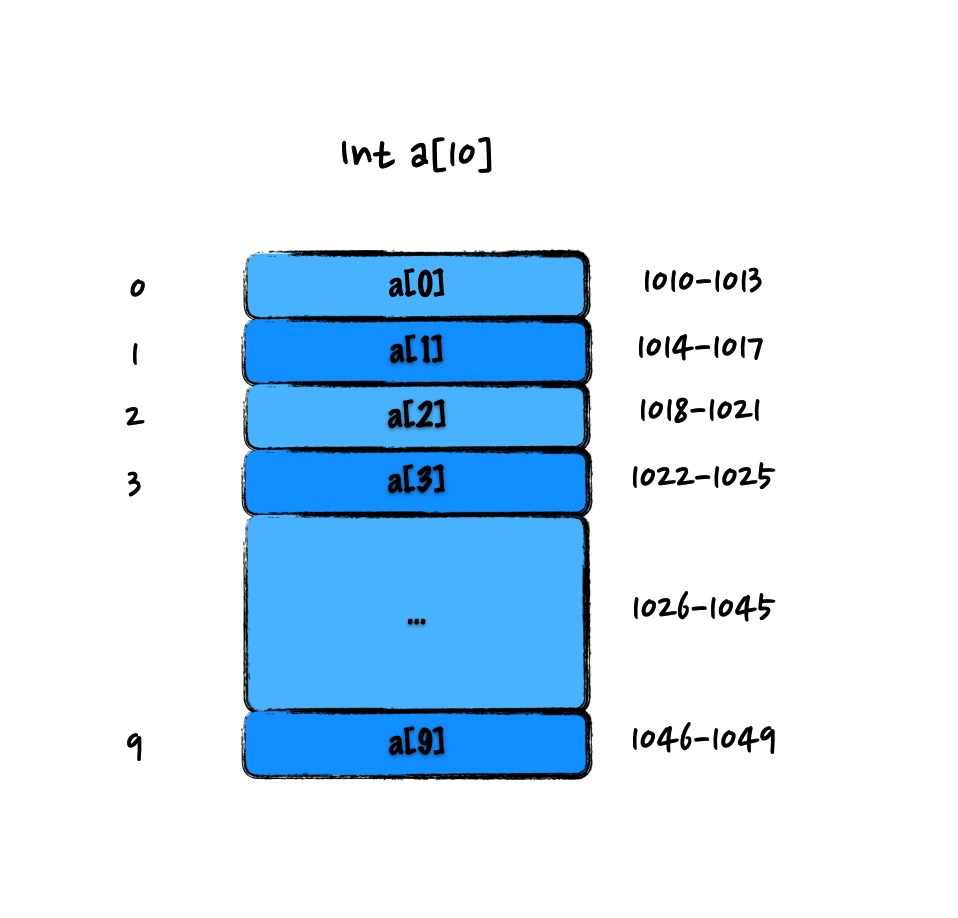
array-a10

计算机会给每个内存单元分配一个地址，并通过地址来访问内存中的数据。对于数组，计算机会在内存中为其申请一段连续的空间，并且会记下索引为 0 处的内存地址为 base_address。当计算机需要随机访问数组中的某个元素时，它会首先通过下面的寻址公式，计算出该元素存储的内存地址:

a[i]_address = base_address + i * data_type_size

此处我们以一个长度为 10 的 int 类型的数组 int[] a = new int[10] 来举例。在图中，计算机给数组 a[10]，分配了一块连续内存空间1010~1049，其中，内存块的首地址为base_address = 1010。其中data_type_size表示数组中每个元素的大小，每个元素占 4 个字节。通过上述公式，可以计算出每个元素在内存中的地址。在计算机中计算内存地址这个过程是很快的，而我们一旦知道了内存地址就可以立即访问到该元素，因此它的时间复杂度是常数级别，为 O(1)。

tip

思考：为什么数组的下标要从 0 开始，而不是从 1 开始？

  1. 如果数组从 1 开始计数，计算数组第 k 个元素的内存地址就会变为: a[k]_address = base_address + (k-1)*type_size。相比于以 0 作为下标的开始，从 1 开始编号会导致每次随机访问数组元素都多了一次减法运算，对于 CPU 来说，就是多了一次减法指令。数组作为非常基础的数据结构，通过下标随机访问数组元素又是其非常基础的编程操作，效率的优化就要尽可能做到极致。所以为了减少一次减法操作，数组选择了从 0 开始编号，而不是从 1 开始。
  2. 也可能是历史原因。C语言设计者用 0 开始计数数组下标，之后的Java、JavaScript等高级语言都效仿了C语言，或者说，为了在一定程度上减少C语言程序员学习Java的学习成本，因此 继续沿用了从 0 开始计数的习惯。实际上，很多语言中数组也并不是从 0 开始计数的，比如Matlab。甚至还有一些语言支持负数下标，比如Python。

查找元素​

如果需要查找数组中是否存在元素 E，从数组开头逐步向后查找。如果数组中的某个元素为目标元素，则停止查找；否则继续搜索直到到达数组的末尾。最坏情况下，搜索的元素在数组最末位，或者数组中不包含目标元素时，需要查找 n 次（n 为数组的长度），此时查找元素的时间复杂度为 O(n)。平均时间复杂度为 (1+2+...n)/n=O(n)。

插入元素​

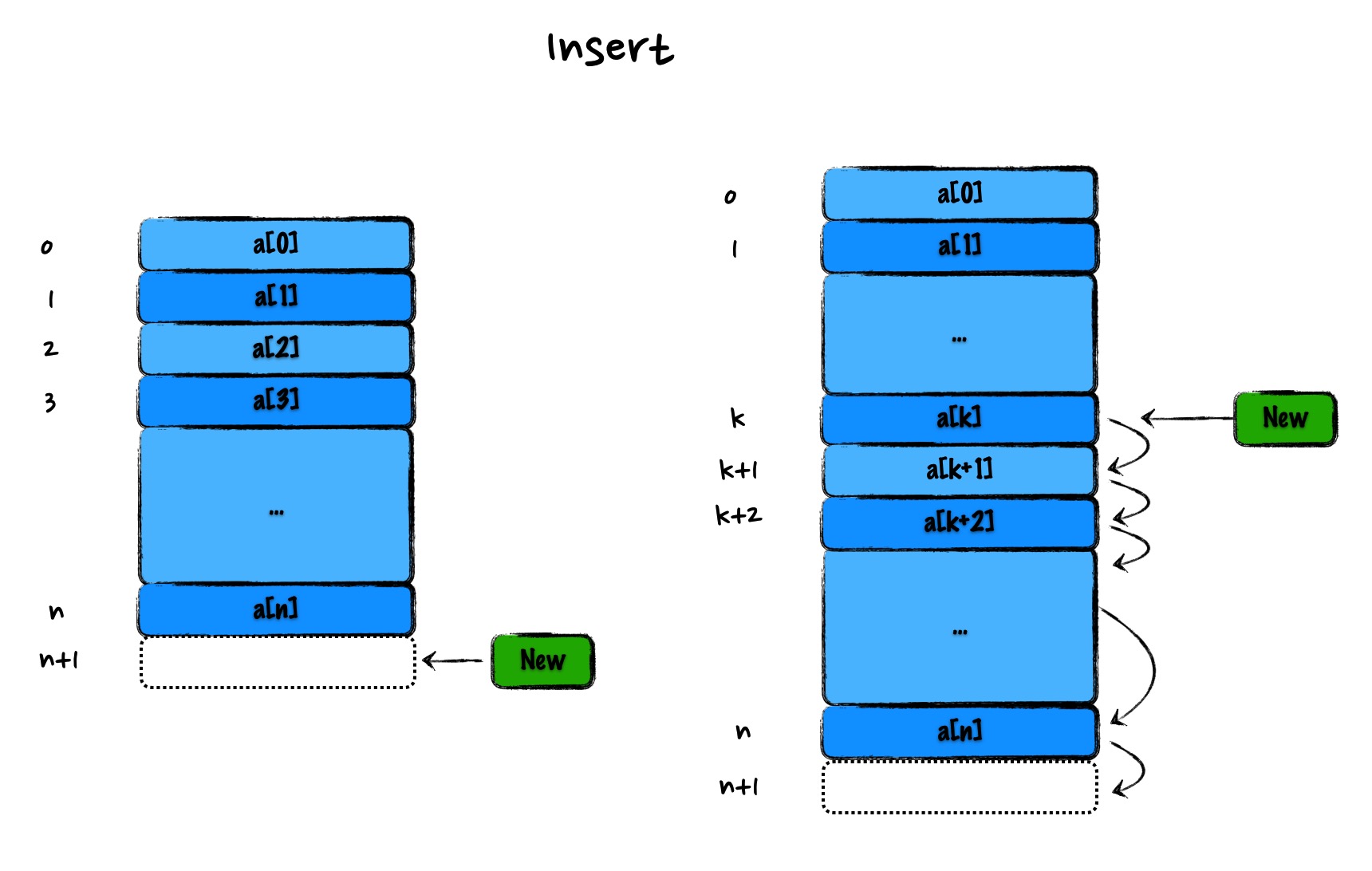
array-insert
  • 在数组末尾插入元素

计算机通过数组的长度和 base_address 计算出即将插入元素的内存地址，然后将该元素插入到指定位置即可，时间复杂度为 O(1)

  • 在数组第 k 位插入元素

如果数组中的元素是无序的，只需要把第 k 位的元素移到最后，然后再在第 k 位插入新元素。如果数组中的元素是有序的，为了保持数据的连续性，需要将第 k~n 这部分的元素都顺序地往后挪一位，为要插入的元素腾出第 k 位，然后进行插入操作。因为在每个位置插入元素的概率是一样的，所以平均情况时间复杂度为 (1+2+...n)/n=O(n)。如果需要频繁地对数组元素进行插入操作，会造成时间的浪费。而另一种数据结构，链表可以有效解决这个问题。

删除元素​

跟插入元素类似，如果我们要删除数组第 k 个位置的元素，为了内存的连续性，也需要搬移数据，不然中间就会出现空洞，内存就不连续了。如果删除数组末尾的数据，则不需要移动数据，时间复杂度为 O(1)。如果删除开头的数据，则为最坏的情况，时间复杂度为 O(n)，n 为数组的长度。所以平均时间复杂度为 (1+2+...n)/n=O(n)。

如何提高删除的效率？

如果不追求数组中数据的连续性，可以将多次删除操作集中在一起执行，以提高删除的效率。例如：数组中存储了 8 个元素：a，b，c，d，e，f，g，h。现在，我们要依次删除a，b，c三个元素。为了避免d，e，f，g，h这几个数据被移动三次，可以先记录下已经删除的数据。每次的删除操作并不是真正地搬移数据，只是记录数据已经被删除。当数组没有更多空间存储数据时，再触发执行一次真正的删除操作，这样就大大减少了删除操作导致的数据搬移。而这也是JVM 标记清除垃圾回收算法的核心思想。

多维数组(multi-dimentional array)​

在上面的介绍中，我们接触到的都是一维数组，通过一个下标就可以找到元素，如：a[0]，获取数组中第一个元素。如果一个数组中的元素都是一维数组，则它是一个二维数组，可以通过数组名[下标1][下标2]的方式获取数组中的元素。如下示例的二维数组 arr，可以通过arr[0][0] 获取元素 1，arr[1][1] 获取元素 5。

const arr = [
  [1, 2, 3],
  [4, 5, 6],
  [7, 8, 9]
];

可以使用两层嵌套的 for 循环遍历整个数组。

//遍历二维数组
for (let i = 0; i < arr.length; i++) {
  //这里是关键，访问arr[i],对arr[i]进行遍历，就是再遍历一维数组
  for (let j = 0; j < arr[i].length; j++) {
    console.log(arr[i][j]);
  }
}

三维数组则是由二维数组作为元素构成的数组。以此类推我们可以得到多维数组(multi-dimentional array)。最常使用的是一维数组和二维数组，其中二维数组经常用来处理矩阵类相关问题，包括矩阵旋转、对角线遍历，以及对子矩阵的操作等。

参考资料​

  1. 数据结构与算法之美, by 王争
  2. 数组和字符串, LeetBook 列表