Skip to main content

对角线遍历

题目​

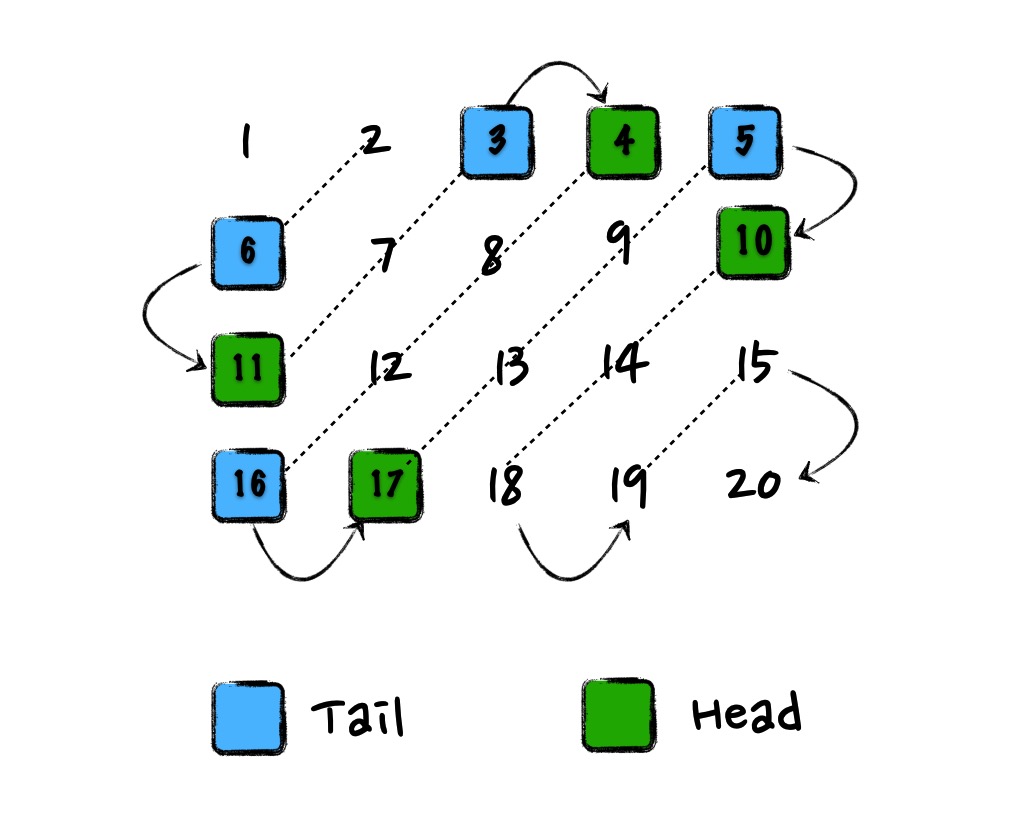
给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

示例 1:

输入:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]

输出:  [1,2,4,7,5,3,6,8,9]

思路​

  • 根据对角线遍历的顺序遍历matrix，使用变量 direction 表示当前对角线的方向，假设当前对角线头部元素为 matrix[i][j]，根据当前对角线方向遍历该对角线：

    1. 向上的对角线，下一个元素是 matrix[i - 1][j + 1]

    2. 向下的对角线，下一个元素是 matrix[i + 1][j - 1]

  • 遍历当前对角线元素直到到达尾部（也是矩阵边界）结束，寻找下一条对角线的头部元素

    1. 向上的对角线头部：如果当前尾部不在矩阵最后一行，则下一个对角线的头部是当前尾部的正下方元素；否则，下一条对角线首部是当前尾部的右边元素

    2. 向下的对角线首部：如果当前尾部不在矩阵最后一行，下一条对角线的首部是当前尾部正下方元素；否则，下一条对角线首部是当前尾部的右边元素

diagonal-traverse1

代码实现​

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
let findDiagonalOrder = function (matrix) {
  if (!matrix || matrix.length === 0) return [];

  // 矩阵的行数
  const N = matrix.length;
  // 矩阵的列数
  const M = matrix[0].length;
  let row = 0,
    column = 0;
  let direction = 1;
  let result = new Array(M * N);
  let r = 0;

  while (row < N && column < M) {
    // 添加当前元素到result
    result[r++] = matrix[row][column];

    // 根据当前元素的位置和对角线方向，计算下一个元素的位置
    let new_row = row + (direction === 1 ? -1 : 1);
    let new_column = column + (direction === 1 ? 1 : -1);

    // 计算当前元素的索引是否在矩阵的范围内，如果不在，说明要找下一个头部元素了
    if (new_row < 0 || new_row === N || new_column < 0 || new_column === M) {
      if (direction === 1) {
        // 向上对角线
        // 如果当前尾部不在矩阵最后一行，则下一个对角线的头部是当前尾部的正下方元素；否则，下一条对角线头部是当前尾部的右边元素。
        row += column === M - 1 ? 1 : 0;
        column += column < M - 1 ? 1 : 0;
      } else {
        // 向下对角线
        // 如果当前尾部不在矩阵最后一行，下一条对角线的头部是当前尾部正下方元素；否则，下一条对角线头部是当前尾部的右边元素。
        column += row === N - 1 ? 1 : 0;
        row += row < N - 1 ? 1 : 0;
      }

      // 切换对角线方向
      direction = 1 - direction;
    } else {
      row = new_row;
      column = new_column;
    }
  }
  return result;
};

复杂度​

  • 时间复杂度：O(N2)，
  • 空间复杂度：O(1)，不使用额外空间。注意：输出数组空间不计入空间复杂度，因为这是题目要求的空间。空间复杂度应该指除了最终数组以外的空间。上一个方法中是中间数组，该方法中只有几个变量