链表基本介绍

链表和数组

链表和数组都属于基础的数据结构--线性表。它们在内存存储上表现不一样，各种操作的效率也不一样。

有了数组为什么还需要链表呢？链表存储数据时，在内存中不一定按照顺序存储，因此能充分利用计算机内存空间。但也同时失去了随机读取的优点。在实现时，每个结点需要增加一个指针域，用于存放下一个元素的地址。

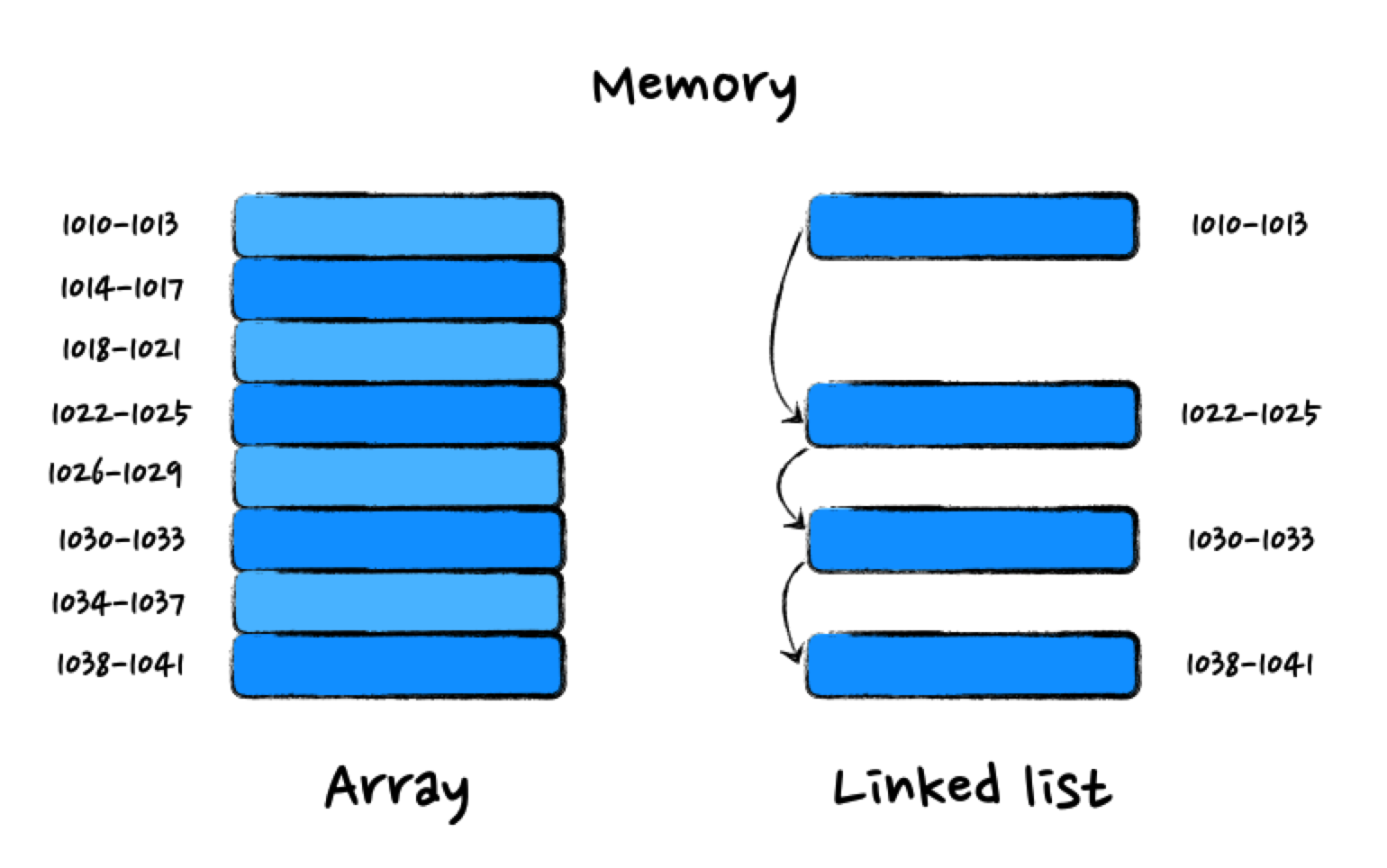
从上图中可以看出，数组需要一块连续的存储空间，对内存要求比较高。如果申请一个 100MB 大小的数组，在内存中没有连续的、足够大的空间时，即便剩余的总可用内存大于 100MB 也会申请失败。

而链表恰恰相反，它不需要一块连续的内存空间，它通过指针将一系列零散的内存小块串联起来使用，所以申请 100MB 大小的链表，根本不会有问题。

几种常见的链表

单链表

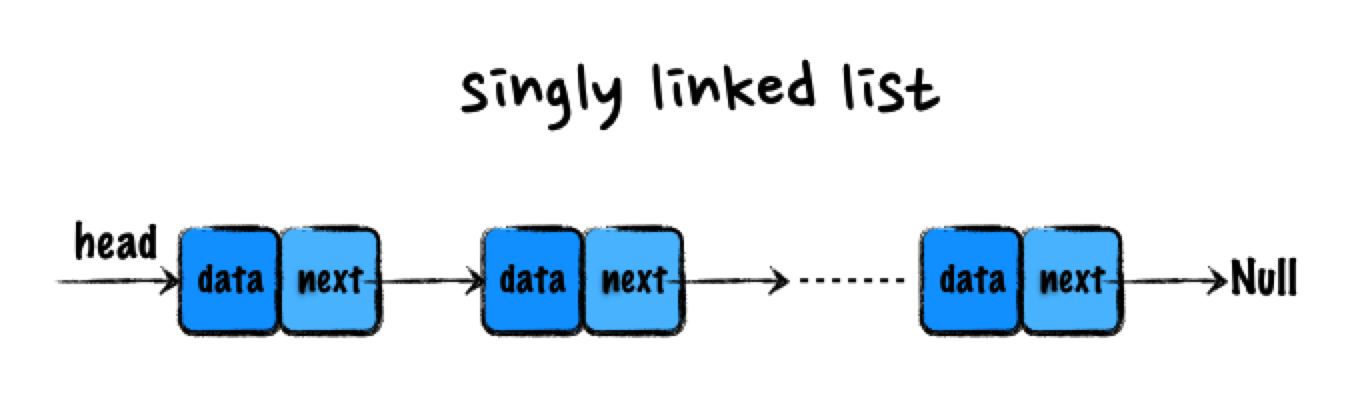
单链表的结构如上图所示，其中的每个结点不仅仅包含值，还包含一个链接到下一个结点的后继指针 next。通过这种方式，单链表将所有结点按顺序组织起来。其中有两个结构很特殊，我们习惯性地称指向链表第一个结点的指针为头指针，最后一个结点为尾结点。其中头指针用来记录链表地基地址，有了它才能遍历整个链表。而尾结点的特殊之处在于其 next 指针不再指向下一个结点，而是指向 NULL，表示这是链表上最后一个结点。

JavaScript

function ListNode(val) {
  this.val = val;
  this.next = null;
}

const head = new ListNode('data1');
head.next = new ListNode('data2');
// ...

Python

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

head = ListNode('data1')
head.next = ListNode('data2')
# ...

数组进行删除和插入操作时，为了保持内存数据的连续性，需要进行大量的数据移动，所以时间复杂度是 O(n)。而在链表中插入或者删除，并不需要移动，因为链表存储空间本身就是不连续的。所以，在链表中插入或删除一个数据是非常快的。

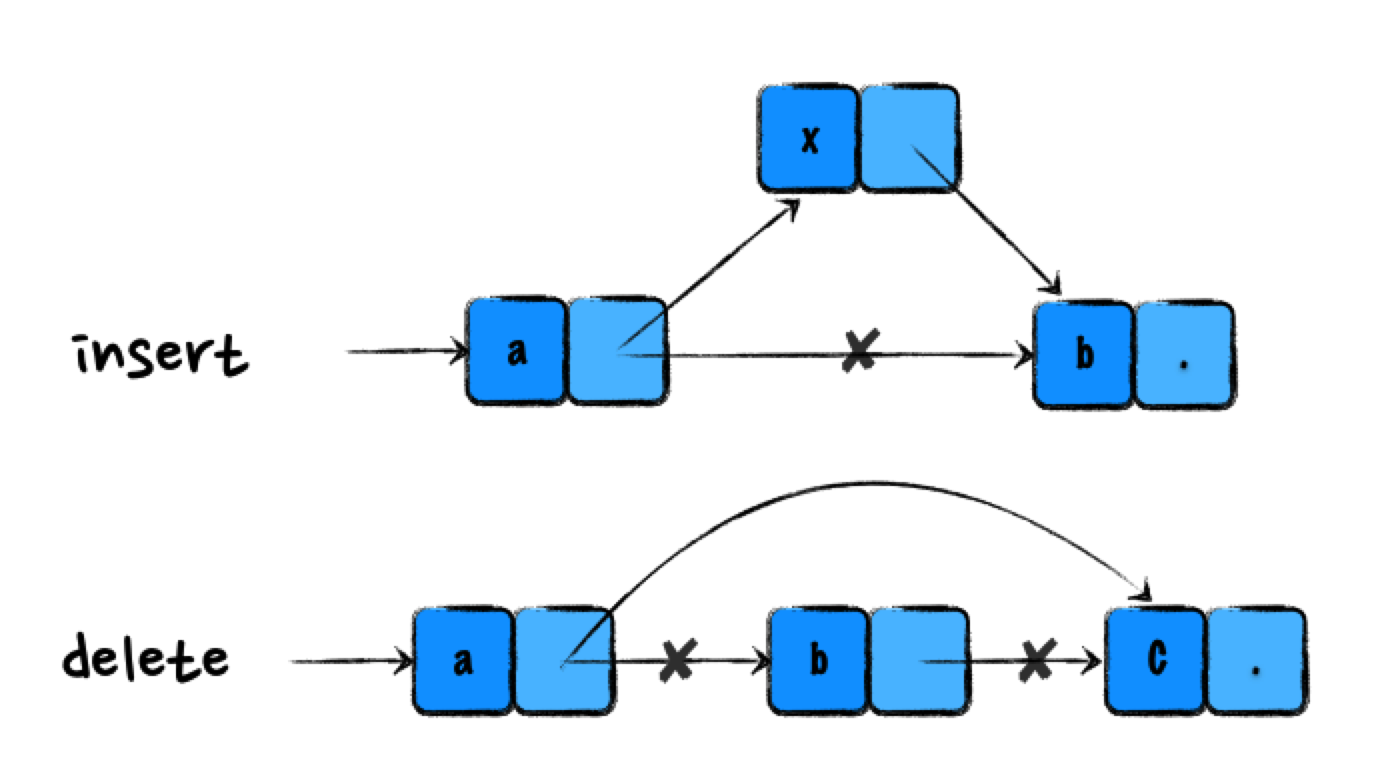
如上图所示，在链表中插入和删除只需要更改几个相邻结点的指针，因此时间复杂度只有 O(1)。

// insert
x.next = a.next;
a.next = x;

// delete
a.next = a.next.next;

但是，当链表需要访问第 k 个结点时，就没有那么高效了。数组是连续存储的，只需要首地址和下标就可以计算出某元素对应的内存地址。而链表是不连续的，只能从头开始一个一个往下数，因此需要 O(n)的时间复杂度。

tip

在具体实现单链表插入和删除操作时，建议使用带头链表

循环链表

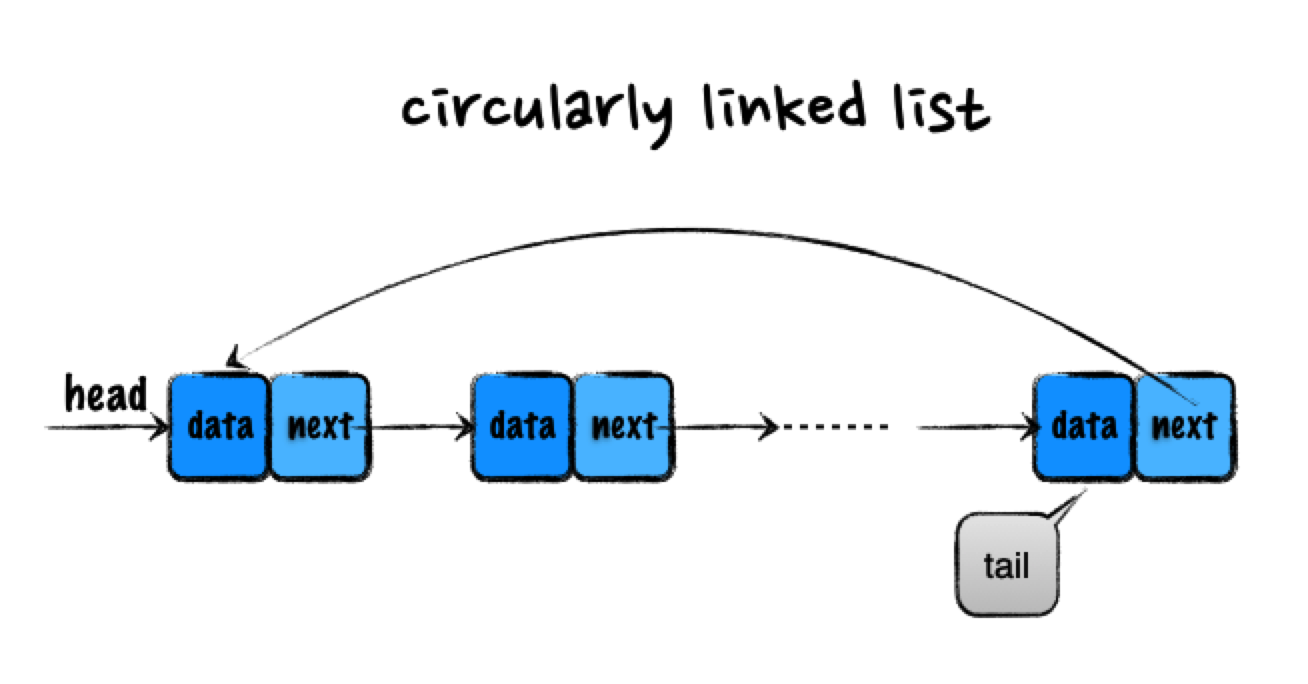
循环链表是一个特殊的单链表，区别仅在于尾结点。不同于单链表尾结点指向 NULL，循环链表尾结点指向头节点。从上图也可以看出，它像一个环一样首尾相连，所以叫做"循环"链表。与单链表相比，循环链表的优点在于从链尾到链头比较方便。当需要处理的数据具有环形结构的时候，就适合采用循环链表。比如著名的约瑟夫问题。

双向链表

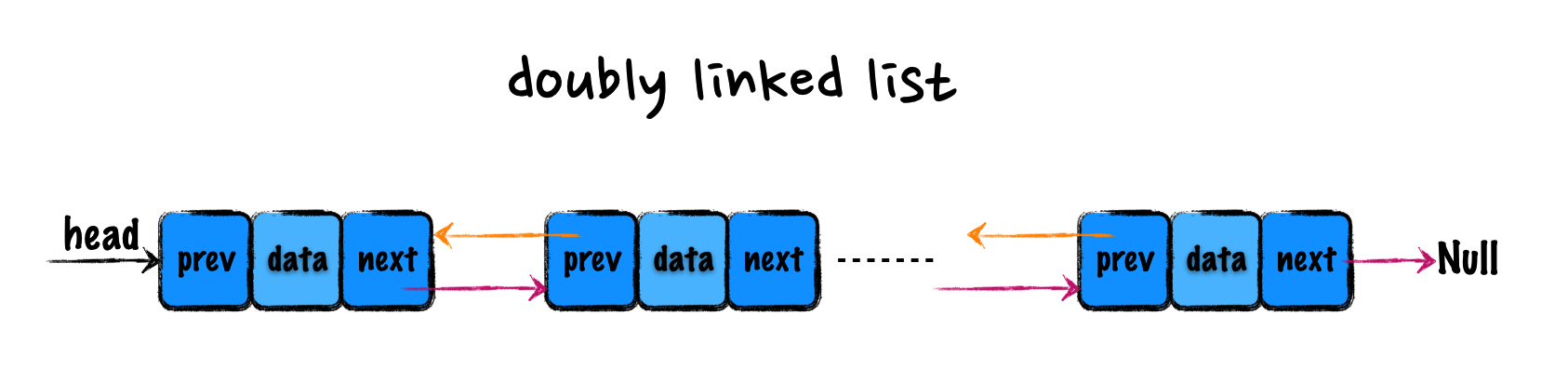
单链表只有一个方向，双向链表，顾名思义，支持两个方向。双向链表中，每一个结点不止一个后继指针 next，还有一个前驱指针 prev，指向该结点的前一个结点。

JavaScript

function ListNode(val) {
  this.val = val;
  this.next = null;
  this.prev = null;
}

const head = new ListNode('data1');
head.next = new ListNode('data2');
head.next.prev = head;
// ...

Python

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None
        self.prev = None

head = ListNode('data1')
head.next = ListNode('data2')
head.next.prev = head
# ...

双向链表

• 缺点
  • 需要多分配一个指针域
  • 执行各种操作后，为了维护双向链表结构，导致复杂度有所增加
• 优点
  • 可以支持 O(1) 时间复杂度的情况下找到前驱结点，正是这样的特点，也使双向链表在某些情况下的插入、删除等操作都要比单链表简单、高效。比如在 LRU 缓存 中的应用

tip

Q: 之前说单链表的插入、删除操作的时间复杂度已经是 O(1) 了，双向链表还能再怎么高效呢？

在单链表中我们对其分析比较偏理论，其实这种说法实际上是不准确的，或者说是有先决条件的。我们先来看删除操作。在实际的开发中，从链表中删除一个数据基本是以下两种情况：

• 删除结点中“值等于某个给定值”的结点，例如 remove_by_value(val), remove_by_index(index)
  • 单链表/双向链表：为了查找到值等于给定值的结点，都需要从头结点开始依次遍历对比，直到找到值等于给定值的结点，然后再通过我前面讲的指针操作将其删除，所以时间复杂度都为 O(n)
• 删除给定指针指向的结点，例如 remove_by_node(node)
  • 单链表：我们已经找到了要删除的结点，但是删除某个结点 q 需要知道其前驱结点，而单链表并不支持直接获取前驱结点，为了找到前驱结点，要从头结点开始遍历链表，直到 p.next = node，说明 p 是 node 的前驱结点，所以时间复杂度为 O(n)
  • 双向链表：因为结点已经保存了前驱结点的指针，不需要再依次遍历，所以时间复杂度为 O(1)

双向循环链表

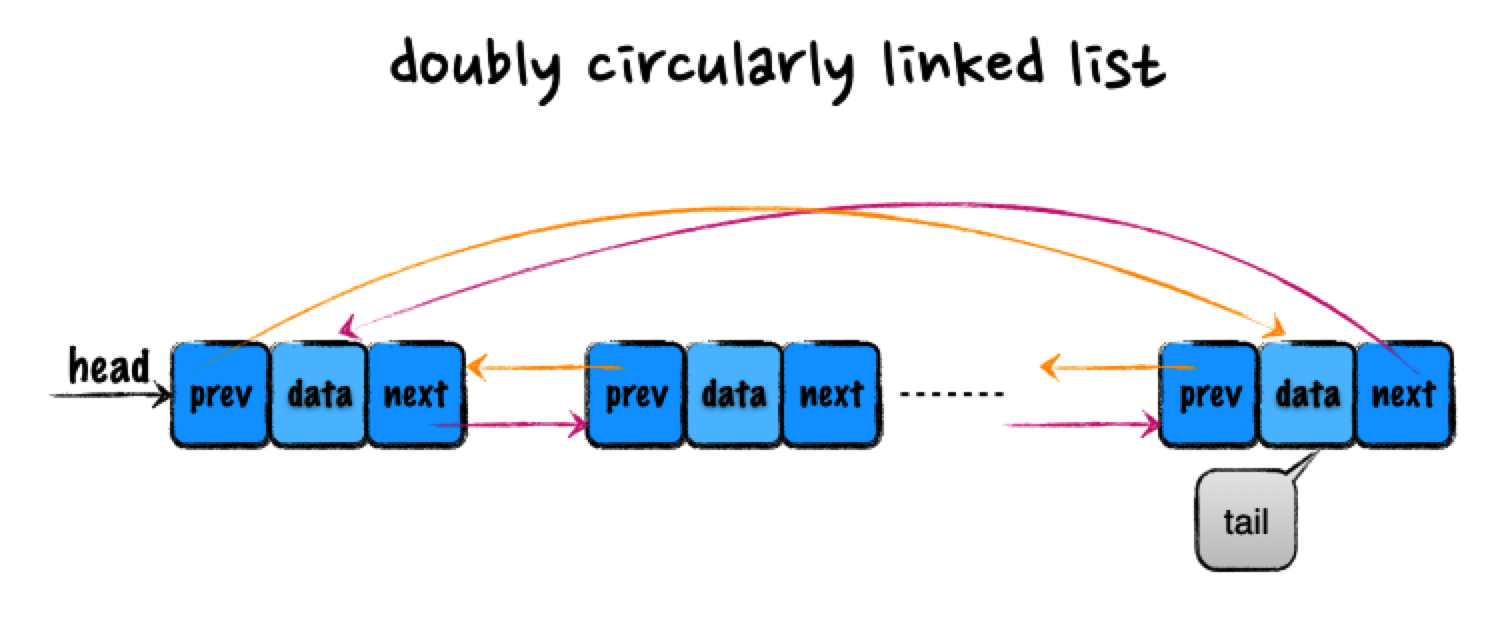
结合了双向链表和循环链表的特点，尾结点的后继指针 next 指向第一个结点，而第一个结点的前驱指针指 prev 向尾结点。

链表和数组的性能对比

时间复杂度	数组	链表
插入删除	O(n)	O(1)
随机访问	O(1)	O(n)

参考资料

1. 数据结构与算法之美, by 王争
2. 链表, leetcode 探索