LRU 缓存
题目
运用你所掌握的数据结构,设计和实现一个 LRU(最近最少使用)缓存机制。它应该支持以下操作:
- 获取数据
get(key)- 如果 key 存在于缓存中,则获取 key 对应的 value(总是正数)
- 否则返回 -1
- 写入数据
put(key, value)- 如果 key 已经存在,则变更其 value
- 如果 key 不存在,则插入该组 key-value
- 当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据,从而为新的数据值留出空间
注意需要在 O(1) 时间复杂度内完成这两种操作。
- JavaScript
- Python
const cache = new LRUCache(2 /* 缓存容量 */);
cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得 key 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得 key 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4
cache = LRUCache(2) # 缓存容量
cache.put(1, 1)
cache.put(2, 2)
cache.get(1) # 返回 1
cache.put(3, 3) # 该操作会使得 key 2 作废
cache.get(2) # 返回 -1 (未找到)
cache.put(4, 4) # 该操作会使得 key 1 作废
cache.get(1) # 返回 -1 (未找到)
cache.get(3) # 返回 3
cache.get(4) # 返回 4
什么是 LRU?
LRU 算法是一种缓存淘汰策略。缓存容量都有限,如果满了就需要删除一些数据,给新的数据腾出空间。那么删除哪些呢?我们期望删除缓存中没什么用的数据,把有用的留着,方便以后继续使用。什么样的数据没用呢?
LRU 策略全称为 Least Recently Used 最近最少使用,即最近最少使用的数据是没用的,会被淘汰。
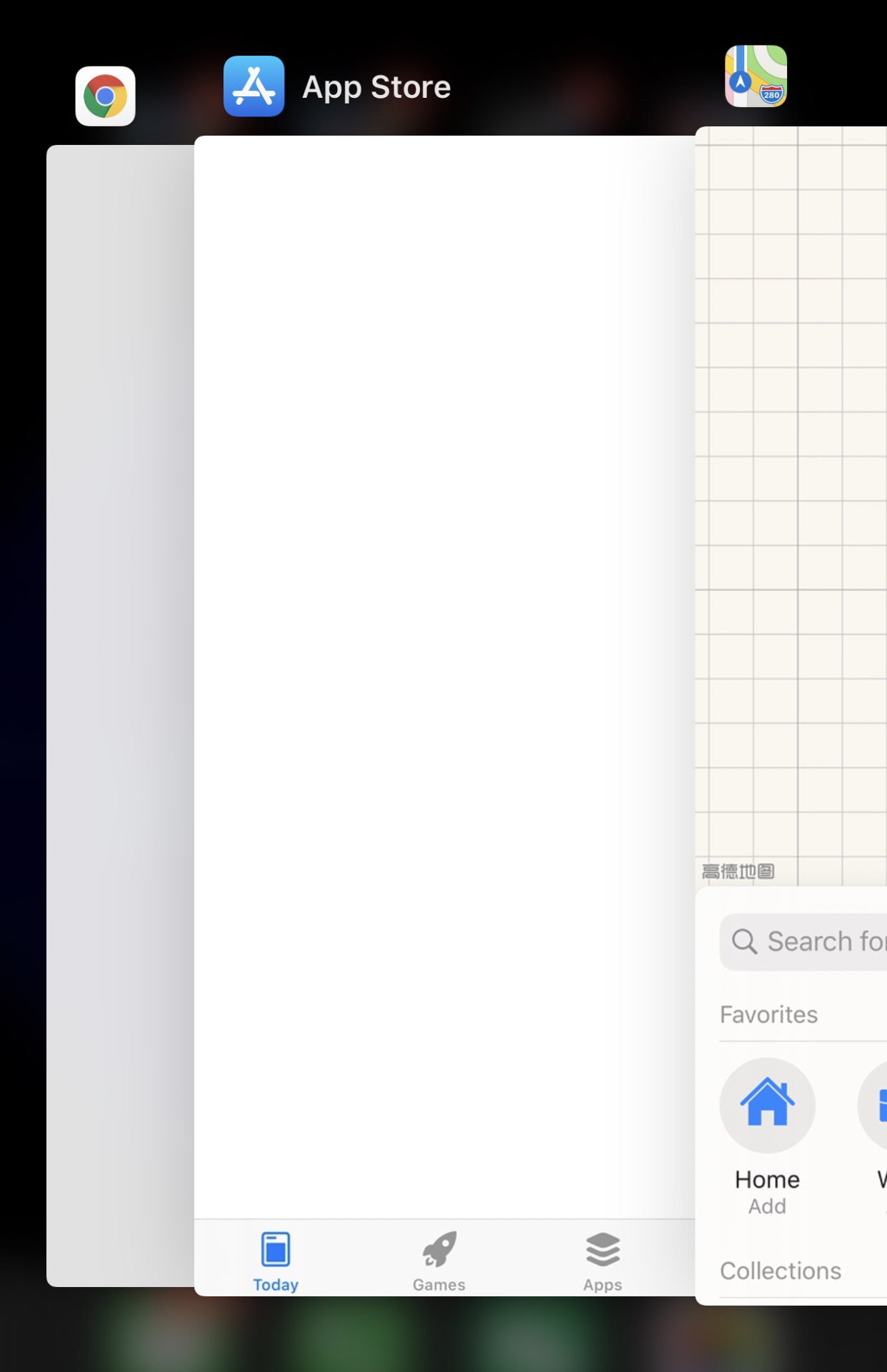
举个例子,比如手机后台程序,先后打开了 Messages, App Store, Chrome, 它们在后台的顺序是这样的:

这时如果又访问了 App Store, App Store会被提前成第一个变成这样:

假设手机只允许后台开 3 个应用程序,现在已经满了。如果再打开一个应用 Maps,就必须关闭一个应用为 Maps 腾出一个位置,关闭哪个呢?
按照 LRU 的策略,最底下的 Messages 会被淘汰,因为它最近最少使用。然后把新打开的应用放到最上面:
思路
分析上面的操作过程,要让 put 和 get 方法的时间复杂度为 O(1),我们可以总结出 cache 这个数据结构必要的条件:查找快,插入快,删除快,有顺序之分。
因为显然 cache 必须有顺序之分,以区分最近使用的和久未使用的数据;而且我们要在 cache 中查找键是否已存在;如果容量满了要删除最后一个数据;每次访问还要把数据插入到队头。
那么,什么数据结构同时符合上述条件呢?
- 哈希表查找快,但是数据无固定顺序;
- 链表有顺序之分,插入删除快,但是查找慢。
所以结合一下,形成一种新的数据结构:哈希链表。LRU 缓存算法的核心数据结构就是哈希链表,它是双向链表和哈希表的结合体。这个数据结构长这样:
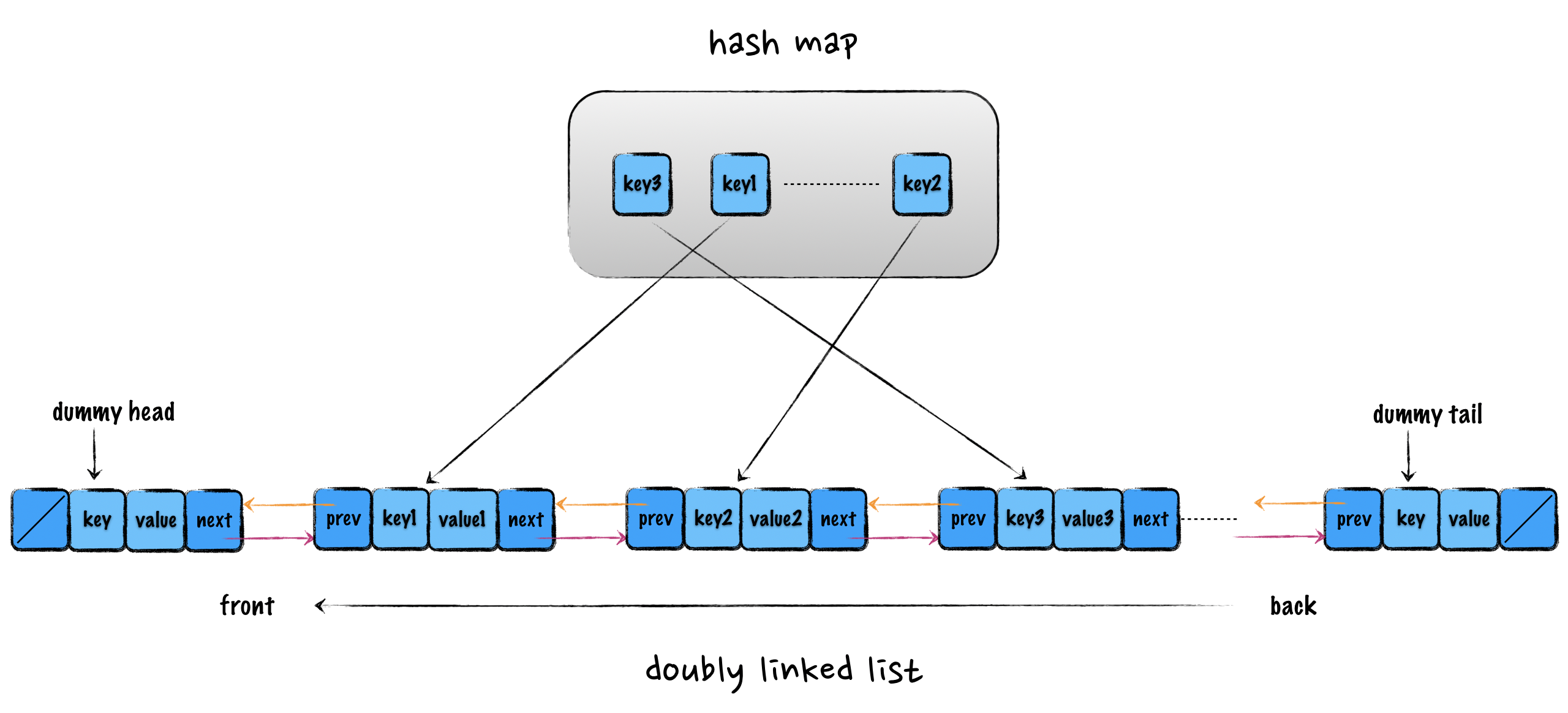
Q: 为什么需要双向链表而不是单链表?
因为需要删除给定指针(hash_map[key])指向的结点,且确保该操作时间复杂度为 O(1)。单链表无法以 O(1) 的时间复杂度获取指定结点的前驱结点。
实际上 cache 的主体还是双向链表,哈希表是为了加快其查找,双向链表节点的个数对应 cache 的 capacity,即双向链表需要一个 size 属性与 capacity 对应。
基本思路:
// key 映射到 Node(key, val)
HashMap<Integer, Node> hashmap;
// Node(k1, v1) <-> Node(k2, v2)...
DoublyLinkedList doublyLinkedList;
int get(int key) {
if (key 不存在) {
return -1;
} else {
将数据 (key, val) 提到开头;
return val;
}
}
void put(int key, int val) {
Node x = new Node(key, val);
if (key 已存在) {
把旧的数据删除;
将新节点 x 插入到开头;
} else {
if (doublyLinkedList 已满) {
删除链表的最后一个数据腾位置;
删除 hashmap 中映射到该数据的键;
}
将新节点 x 插入到开头;
hashmap 中新建 key 对新节点 x 的映射;
}
}
代码实现
- JavaScript
- Python
function ListNode(key, value) {
this.key = key;
this.value = value;
this.next = null;
this.prev = null;
}
function DoublyLinkedList() {
this.dummyHead = new ListNode();
this.dummyTail = new ListNode();
this.dummyHead.next = this.dummyTail;
this.dummyTail.prev = this.dummyHead;
this.size = 0;
}
/**
* 双向链表头部添加一个新结点
* @param {ListNode} node
*
*/
DoublyLinkedList.prototype.addAtHead = function (node) {
node.next = this.dummyHead.next;
node.prev = this.dummyHead;
this.dummyHead.next = node;
node.next.prev = node;
this.size++;
};
/**
* 删除双向链表最后一个结点,并返回该结点
* @return {ListNode}
*
*/
DoublyLinkedList.prototype.deleteAtTail = function () {
const last = this.dummyTail.prev;
this.dummyTail.prev = last.prev;
last.prev.next = last.next;
last.prev = null;
last.next = null;
this.size--;
return last;
};
/**
* 删除双向链表中的某个结点。结点一定存在
* @param {ListNode} node
*
*/
DoublyLinkedList.prototype.delete = function (node) {
node.prev.next = node.next;
node.next.prev = node.prev;
node.next = null;
node.prev = null;
this.size--;
};
/**
* @param {number} capacity
*/
var LRUCache = function (capacity) {
this.capacity = capacity;
this.hashmap = {};
this.doublyLinkedList = new DoublyLinkedList();
};
/**
* @param {number} key
* @return {number}
*/
LRUCache.prototype.get = function (key) {
if (this.hashmap[key] === undefined) {
return -1;
}
const val = this.hashmap[key].value;
// 利用put方法把该数据提前
this.put(key, val);
return val;
};
/**
* @param {number} key
* @param {number} value
* @return {void}
*/
LRUCache.prototype.put = function (key, value) {
const node = new ListNode(key, value);
if (this.hashmap[key] !== undefined) {
this.doublyLinkedList.delete(this.hashmap[key]);
this.doublyLinkedList.addAtHead(node);
this.hashmap[key] = node;
} else {
if (this.doublyLinkedList.size === this.capacity) {
const last = this.doublyLinkedList.deleteAtTail();
this.hashmap[last.key] = undefined;
}
this.doublyLinkedList.addAtHead(node);
this.hashmap[key] = node;
}
};
/**
* Your LRUCache object will be instantiated and called as such:
* var obj = new LRUCache(capacity)
* var param_1 = obj.get(key)
* obj.put(key,value)
*/
class ListNode:
def __init__(self, key: int, value: int):
self.key = key
self.value = value
self.next = None
self.prev = None
class DoublyLinkedList:
def __init__(self):
self.dummy_head = ListNode(0, 0)
self.dummy_tail = ListNode(0, 0)
self.dummy_head.next = self.dummy_tail
self.dummy_tail.prev = self.dummy_head
self.size = 0
def add_at_head(self, node: ListNode) -> None:
node.next = self.dummy_head.next
node.prev = self.dummy_head
self.dummy_head.next = node
node.next.prev = node
self.size += 1
def delete_at_tail(self) -> ListNode:
last_node = self.dummy_tail.prev
self.dummy_tail.prev = last_node.prev
last_node.prev.next = last_node.next
last_node.prev = None
last_node.next = None
self.size -= 1
return last_node
def delete(self, node: ListNode) -> None:
node.prev.next = node.next
node.next.prev = node.prev
node.next = None
node.prev = None
self.size -= 1
class LRUCache:
def __init__(self, capacity: int):
self.capacity = capacity
self.hash_map = {}
self.doubly_linked_list = DoublyLinkedList()
def get(self, key: int) -> int:
if key not in self.hash_map:
return -1
val = self.hash_map[key].value
# Use the put method to front the data
self.put(key, val)
return val
# Key code
def put(self, key: int, value: int) -> None:
node = ListNode(key, value)
if key in self.hash_map:
self.doubly_linked_list.delete(self.hash_map[key])
elif self.doubly_linked_list.size == self.capacity:
last_node = self.doubly_linked_list.delete_at_tail()
del self.hash_map[last_node.key]
self.doubly_linked_list.add_at_head(node)
self.hash_map[key] = node
# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)
复杂度
- 时间复杂度:O(1)
- 空间复杂度:O(n)