Skip to main content

归并排序

题目​

给定一个整数数组  nums，使用归并排序将该数组升序排列。

示例 1：

输入：[5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：[5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

提示：

  • 1 <= A.length <= 10000
  • -50000 <= A[i] <= 50000

思路​

将待排数组逐步二分，当二分长度为 1 的时候停止。然后再将分好的数组排序，并逐步合并为一个有序的数组：

  1. 先分割再合并
  2. 使用递归进行分割
  3. 使用迭代或者递归进行合并
  4. 如何尽量减少辅助内存的使用
  5. 排序的顺序从宏观上来说是从左到右逐渐有序的

归并过程如下图所示：

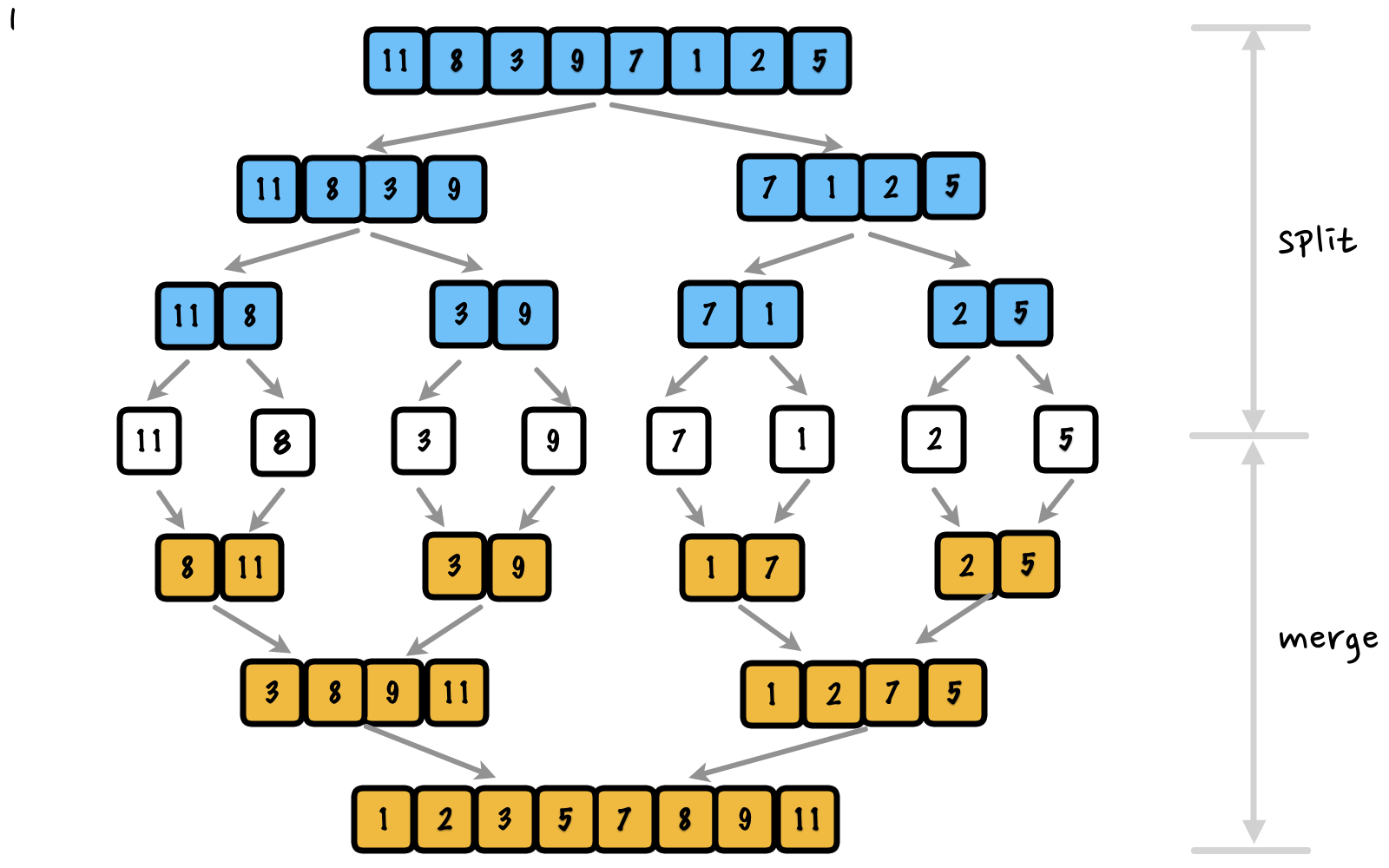
实现​

方法一：使用 slice 分割​

分割数组时直接将数组分割为两个新数组，合并时直接合并数组。

  • 优点：思路简单，写法简单
  • 缺点：空间复杂度略高，需要复制多个数组
/**
 * @param {number[]} nums
 * @return {number[]}
 */
function sortArray(nums) {
  if (nums.length < 2) {
    // 当数组为一个元素时停止
    return nums;
  }
  let mid = nums.length >> 1;
  let left = sortArray(nums.slice(0, mid)); // 对原始数组递归二分
  let right = sortArray(nums.slice(mid));
  return merge(left, right);
}

function merge(left, right) {
  let ans = [];
  let i = 0;
  let j = 0;
  while (i < left.length && j < right.length) {
    // 对二分好的数据排序整合在一起
    left[i] > right[j] ? ans.push(right[j++]) : ans.push(left[i++]);
  }
  // 处理剩余元素
  while (i < left.length) {
    ans.push(left[i++]);
  }
  while (j < right.length) {
    ans.push(right[j++]);
  }
  return ans;
}

递归版 merge，在数据量比较大的时候会内存溢出，test case:

function merge(left, right) {
  if (!left.length) return right;
  if (!right.length) return left;
  let ans = [];
  if (left[0] > right[0]) {
    ans.push(right[0], ...merge(left, right.slice(1)));
  } else {
    ans.push(left[0], ...merge(left.slice(1), right));
  }
  return ans;
}

方法二：使用 left, right 索引分割​

记录数组的索引，使用 left、right 两个索引来限定当前分割的数组。

  • 优点：空间复杂度低，只需一个 ans 辅助空间，不需要拷贝数组
  • 缺点：sortArray 函数略显复杂
function sortArray(nums, from = 0, to = nums.length - 1) {
  if (from === to) {
    return [nums[from]];
  }
  let mid = from + ((to - from) >> 1);
  let left = sortArray(nums, from, mid);
  let right = sortArray(nums, mid + 1, to);
  return merge(left, right);
}

分析​

空间复杂度​

由上面的算法可以看出，merge 函数中使用了一个临时数组 result，空间复杂度为 O(n)，但是 result 数组在每次合并后都会被释放，在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。

时间复杂度​

归并排序 merge 操作的时间复杂度为 O(n)，在快排我们也讲过递归操作的递归深度为 logn，因此归并排序的时间复杂度为 O(nlogn)。归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。

虽然归并排序可以做到无论是什么情况时间复杂度都是 O(nlogn)，但是由于它的空间复杂度较高，当数据量较大的时候，内存占用量过大，因此归并排序只有在数据量较小，比如说 1k，2k 的时候可能会使用到，当数据量较大时还是会使用快速排序。

稳定性​

归并排序的稳定性取决于 merge 函数，当我们在比较left[i] <= right[j]的时候，如果遇到相同的元素，让左边区间的元素先进 result，这样可以保证归并排序是个稳定的排序算法。