堆排序
基本概念
堆是一个完全二叉树,堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
- “大顶堆”:每个节点的值都大于等于子树中每个节点值的堆
- “小顶堆”:每个节点的值都小于等于子树中每个节点值的堆
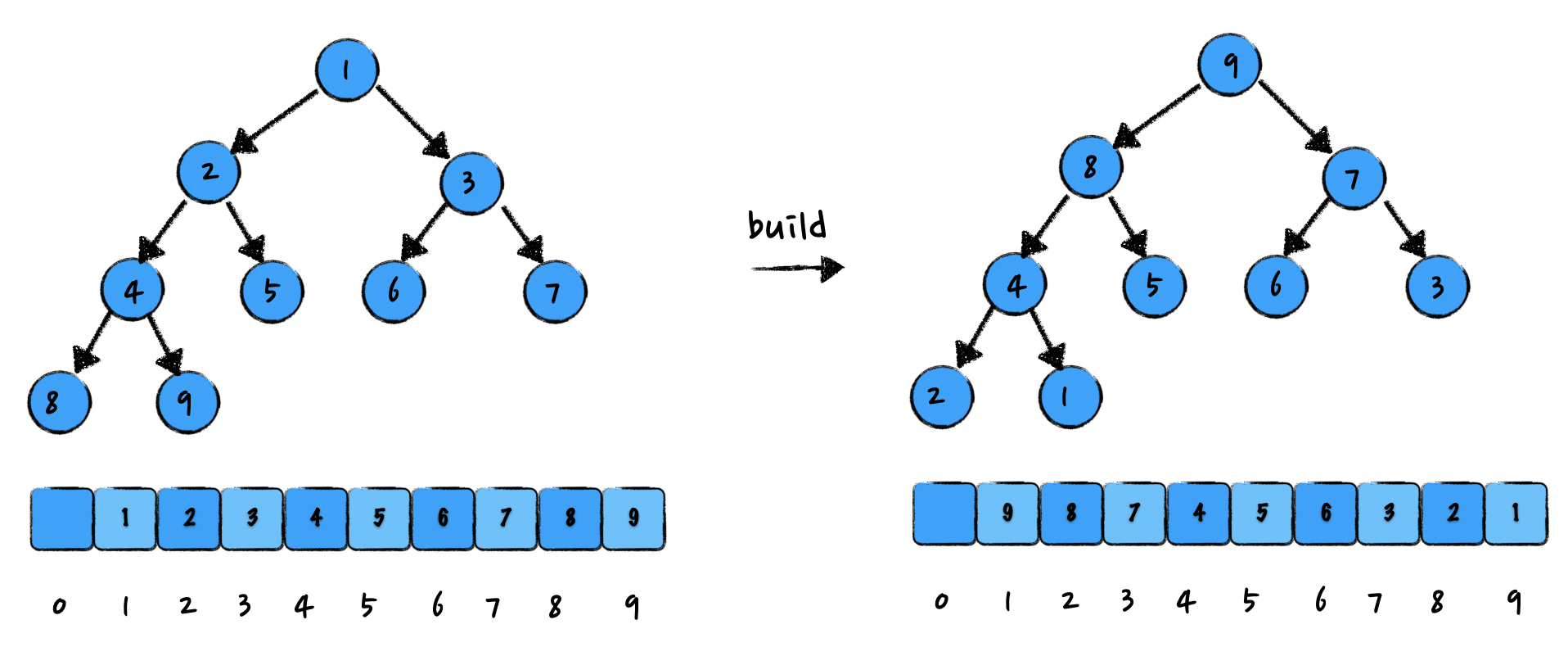
堆排序的关键就是将代排序列调整为堆。堆排序的过程可以分为建堆和排序两个步骤。
在本节中为了更好的计算,让数据在数组中的存储的下标从 1 开始,这样可以保证数组中下标为 i 的节点的左子节点,就是下标为 i*2 的节点,右子节点就是下标为 i*2+1 的节点,父节点就是下标为 i/2 的节点。
建堆
思路
将序列调整为一个大顶堆,首先从后往前处理数组,找到第一个非叶子节点,然后比较其子节点,如果子节点的值大于当前节点,就将当前节点和最大的子节点交换。然后重复此过程,直到根节点调整完毕后结束。

由完全二叉树的特点不难得出,从 1 到 n/2 的元素都是非叶子节点,n/2+1 到 n 都是叶子节点。(其中 n/2 向下取整)
实现
通过上面的描述,建堆的算法实现如下所示:
// 元素交换
function swap(arr, i, j) {
[arr[i], arr[j]] = [arr[j], arr[i]];
}
// 遍历非叶子节点
function buildHeap(arr, n) {
for (let i = n >> 1; i >= 1; --i) {
heapify(arr, n, i); // a为数组 n为数组的长度 i为非叶子节点下标
}
}
function heapify(arr, n, i) {
while (true) {
let maxPos = i;
if (i * 2 <= n && arr[i] < arr[i * 2]) {
// 与其做节点比较
maxPos = i * 2;
}
if (i * 2 + 1 <= n && arr[maxPos] < arr[i * 2 + 1]) {
// 用当前节点或左节点和右节点比较
maxPos = i * 2 + 1;
}
if (maxPos === i) break;
swap(arr, i, maxPos);
i = maxPos;
}
}
排序
思路
经过上面建堆的过程,我们会获得一个大顶堆,大顶堆的根元素是所有元素最大的,我们可以将其与最后一个元素交换,然后对剩下的n-1个元素进行排序。最后一个元素成为根元素后和其左右子元素比较,与较大的交换,然后再将根元素与最后一个元素交换,依次类推,直到剩余一个元素。排序的过程下图所示:
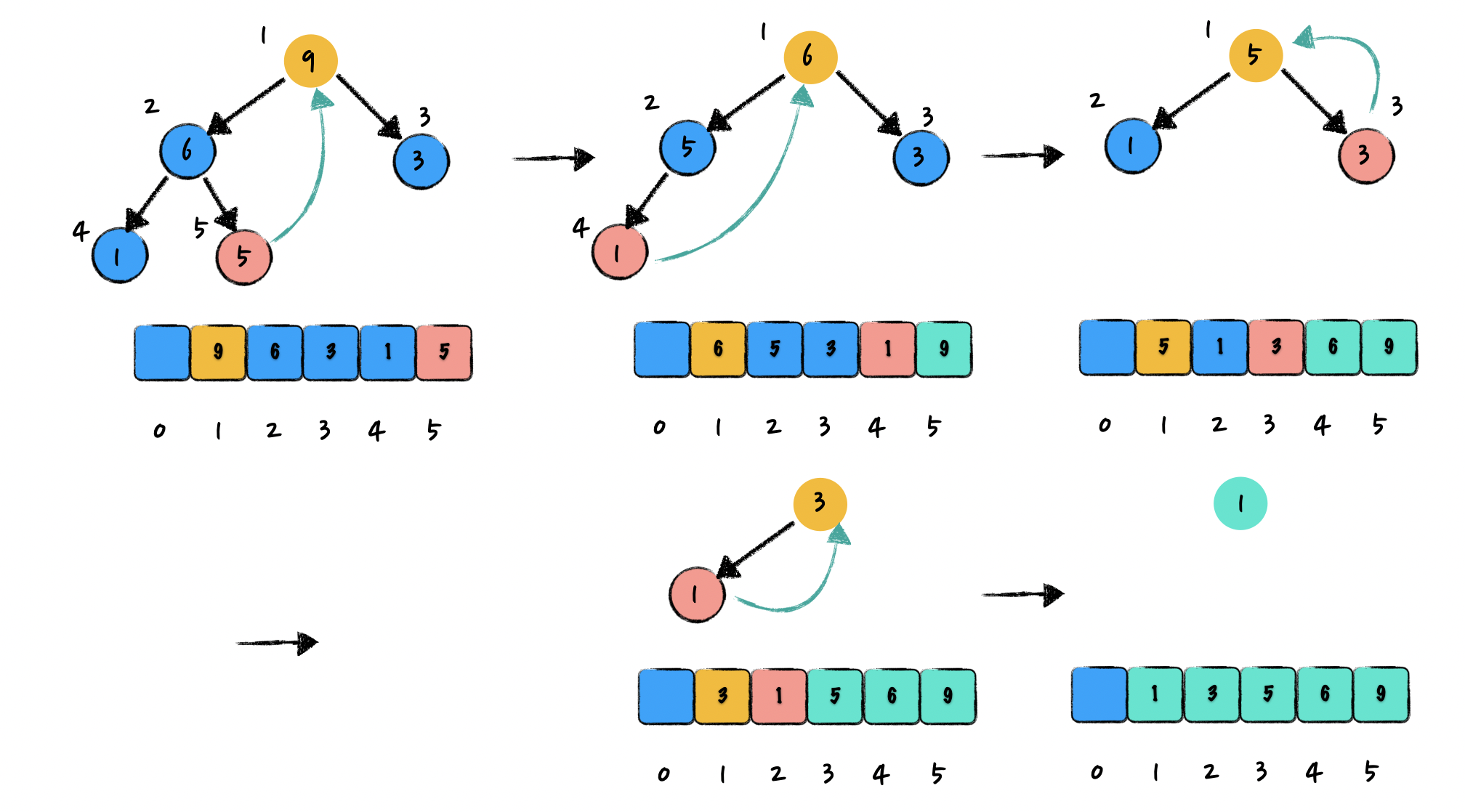
实现
通过建堆的算法实现和排序的过程,得出的堆排序算法如下:
// 元素交换
function swap(arr, i, j) {
[arr[i], arr[j]] = [arr[j], arr[i]];
}
// 遍历非叶子节点,建堆
function buildHeap(arr, n) {
for (let i = n >> 1; i >= 1; --i) {
heapify(arr, n, i); // a为数组 n为数组的长度 i为非叶子节点下标
}
}
// 父子元素比较大小
function heapify(arr, n, i) {
while (true) {
let maxPos = i;
if (i * 2 <= n && arr[i] < arr[i * 2]) {
// 与其做节点比较
maxPos = i * 2;
}
if (i * 2 + 1 <= n && arr[maxPos] < arr[i * 2 + 1]) {
// 用当前节点或左节点和右节点比较
maxPos = i * 2 + 1;
}
if (maxPos === i) break;
swap(arr, i, maxPos);
i = maxPos;
}
}
// 排序
function heapSort(arr, length) {
buildHeap(arr, length); // 建堆
for (let n = length; n > 1; n--) {
swap(arr, 1, n); // 交换根元素和最后一个元素
heapify(arr, n, 1);
}
}
arr.unshift(0); // 首部添加一个元素0
heapSort(arr, arr.length);
arr.shift(); // 删除第一个元素
分析
空间复杂度
堆排序的过程,只需要个数级的辅助空间,因此堆排序是空间复杂度为O(1)的原地排序算法。
时间复杂度
由上面的代码不难看出,堆排序的时间复杂度 = 建堆时间复杂度 + 排序时间复杂度。
建堆的时间复杂度:建堆的主要工作是遍历非叶子节点和调换父子节点,这一过程也被称为堆化。也就是说堆化最多从树的倒数第二层到根元素都是需要的,而每个节点堆化的过程中,需要比较和交换的节点个数和这个节点的高度 k 成正比,如下图:

由上图可以看出高度为 1(倒数第二层)的非叶子节点为 2^(h-1)个,每个节点执行 heapify 函数中的 while 只需要执行 1 遍,而高度为 2 的非叶子节点,每个节点执行 heapify 函数 while 需要执行 2 遍,依次类推,我们发现将每个节点的高度求和,得出的就是建堆的时间复杂度。
求和公式为:
计算该公式可以使用错位相减法:
让右错一位,然后减去
得到一个等比数列如下:
然后等比数列求和得出:
h 为树的高度 ,将 h 代进去,得出建堆的时间复杂度为 O(n)。
排序时间复杂度: 由算法可以看出排序时间复杂度为 for 循环时间 * 并为每个节点进行堆化的时间,堆化的时间复杂度为 O(logn),因此排序的时间复杂度为 O(nlogn)。
堆排序的时间复杂度 = 建堆时间复杂度 + 排序时间复杂度 = O(n) + O(nlogn),因此堆排序得时间复杂度为 O(nlogn)。并且时间复杂度和初始序列顺序无关,时间复杂度始终为 O(nlogn)。
稳定性
堆排序是不稳定的排序算法,因为在排序的过程中会选择最后一个元素和根元素交换,一旦交换后堆稳定,不需要再交换,此时如果子树中有和根元素相同的元素,则改变了初始顺序,例如:9、5、4、5 中最后的一个 5 和 9 交换后堆稳定,最后的一个 5 输出,显然不稳定。
缺点
虽然堆排序的时间复杂度始终是 O(nlogn),并且空间复杂度为 O(1),而快速排序确只有最好的情况时间复杂度为 O(nlogn),并且空间复杂度为 O(logn),但是在实际开发中,快速排序却比堆排序性能表现的更好。
首先,堆排序在堆化的过程中,数据访问的方式一般是跳着访问,而不是像快速排序那样,局部顺序访问,所以,这样加重 CPU 缓存的负担。
其次,相比于快速排序,堆排序算法的数据交换次数要更多。快速排序元素的交换次数为初始序列的逆序数,而堆排序在建堆的时候会破坏初始序列的逆序数。例如当一个有序的初始序列,通过建大顶堆使得数据变得无序,如下图: