Skip to main content

冒泡排序

思想​

冒泡排序每次冒泡操作都会对相邻的两个元素进行比较，如果相邻元素左侧较大，则交换两个元素，一趟冒泡排序最大的元素会被放到最后。在这个过程中，大的元素会像石头一样沉入水底，而小的元素就像是气泡一样向上浮动，所以这个排序被形象的称为冒泡排序。

下面使用一个例子，来演示下冒泡排序的整个过程。首先设定一组待排序数据 5, 4, 6, 2, 1, 3。并将其从小到大进行排序。第一次冒泡操作的详细过程如下图所示：

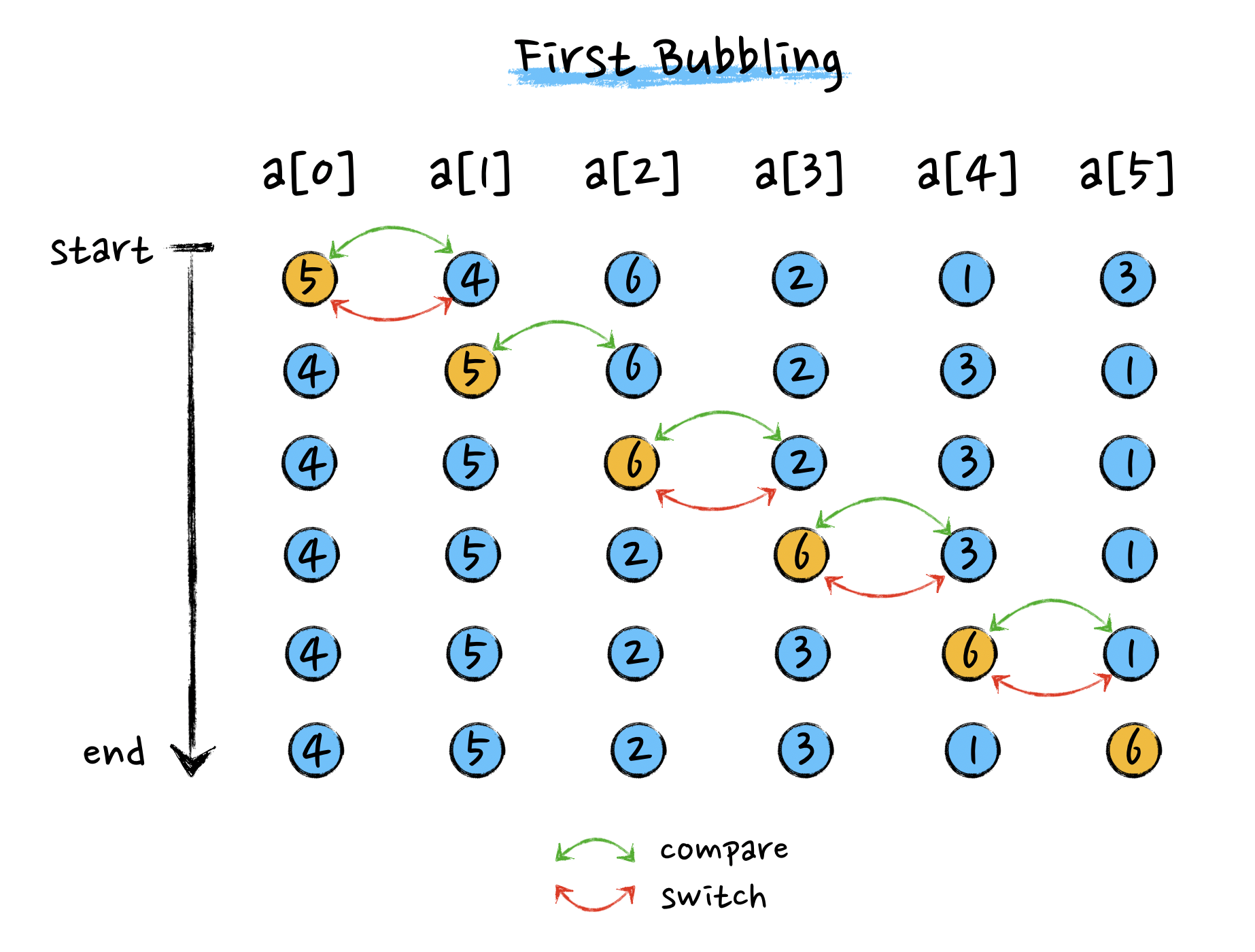
zzmUUK

通过上图可以看出，经过一趟冒泡操作，待排数据中最大的值被放到了正确的位置上。要想完成所有数据的排序，我们只要进行 6 次这样的冒泡操作就行了。

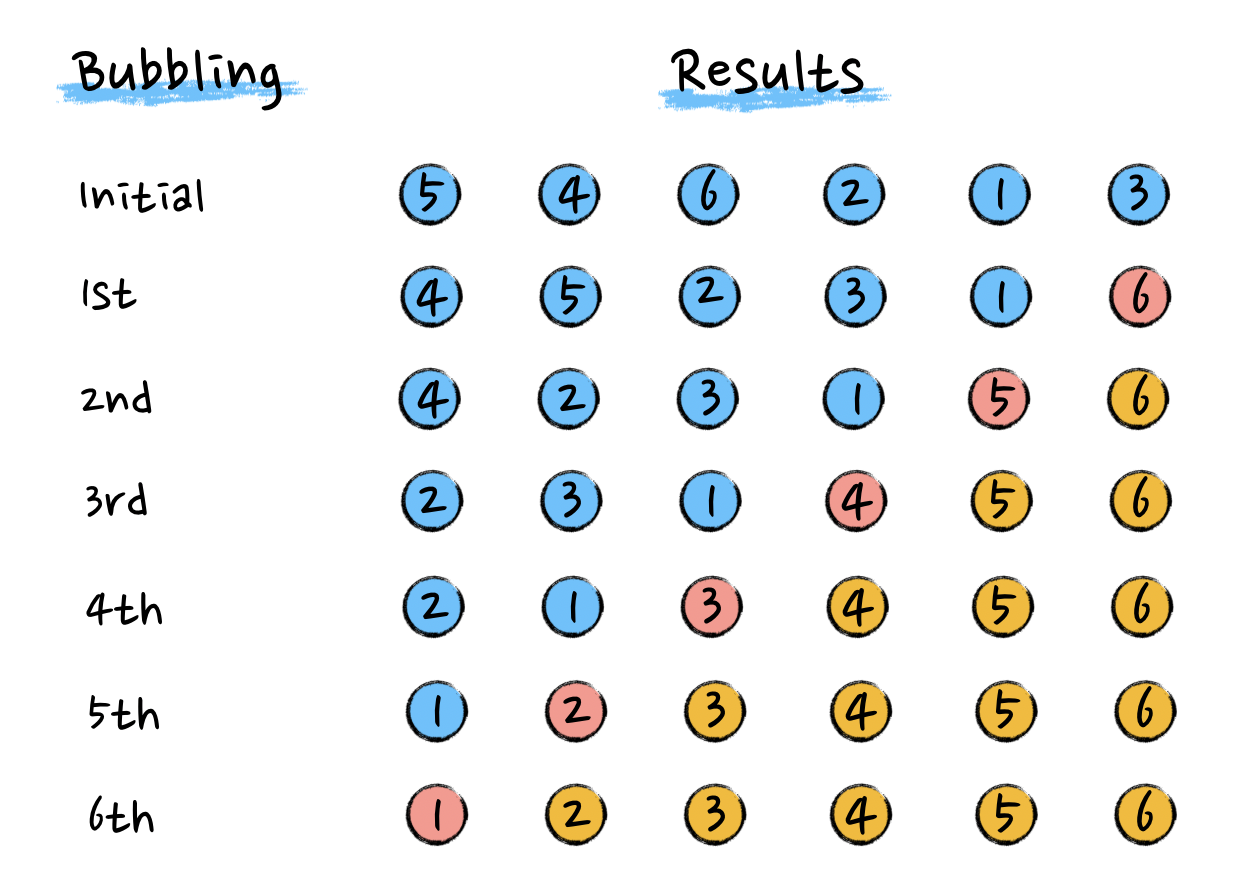
IPpQxY

实现​

冒泡排序需要内外两层循环，其中外层循环用于代表冒泡次数，内层循环用来比较相邻两个元素，当左侧元素小于右侧元素时进行交换。

tip

优化：当某次冒泡中一次数据交换都没有发生时，说明已经完全有序，不用再继续执行后续的冒泡。

具体的实现如下所示：

// 相邻两个元素交换
function swap(nums, a, b) {
  let tmp = nums[a];
  nums[a] = nums[b];
  nums[b] = tmp;
}

/**
 * @param {number[]} nums
 * @return {number[]}
 */
var sortArray = function (nums) {
  const length = nums.length;

  for (let i = 0; i < length; i++) {
    let hasSwitched = false; // 设置标志位，当为false表示没有交换，此时应该返回数组
    for (let j = 0; j < length - i - 1; j++) {
      // 后面是和j+1个元素比较，所以还需要再减一
      if (nums[j] > nums[j + 1]) {
        // 保证冒泡是稳定的算法
        swap(nums, j, j + 1);
        hasSwitched = true;
      }
    }
    if (!hasSwitched) return nums;
  }

  return nums;
};

分析​

空间复杂度​

冒泡的过程只涉及相邻数据的交换操作，只需要常量级的辅助空间，所以它的空间复杂度为 O(1)。

时间复杂度​

  • 最好的情况是待排序列完全有序，没有元素交换，此时只需要一趟冒泡就可以跳出循环（参考冒泡优化），所以时间复杂度为 O(n)。
  • 最坏的情况为待排序列倒序，需要n-1趟冒泡，每趟排序要进行n-i次比较，所以时间复杂度为 O(n^2)。
  • 平均时间复杂度为 n(n^2)。
    • 平均时间复杂度如果使用概率论来计算相对来说比较复杂，我们可以通过逆序数的概念来进行分析。在冒泡排序中会比较相邻两个元素，每次交换元素，序列的逆序数就会减 1。所以冒泡排序的过程就是一种减少逆序数的过程，当逆序数减少到 0 时，序列完全有序。
    • 前面提到，完全有序的序列的逆序数为 0，排序时不需要交换。而倒序的逆序数为 n*(n-1)/2，则需要调用n*(n-1)/2 次 swap 方法。一个序列的逆序数的平均数为n*(n-1)/4，我们取平均交换的次数约为n*(n-1)/4，来表示初始逆序数的平均情况，则需要 n*(n-1)/4 次交换操作，而比较操作肯定要比交换操作多（比较了不一定交换，平均比较次数要大于n*(n-1)/4），所以平均时间复杂度也是 O(n^2)。

稳定性​

从算法实现中可以看出，交换只会出现在相邻两个元素中。为了保证稳定性，当相邻的两个元素大小相等的时候，我们不做交换。那么相同大小的数据在排序前后的顺序就不会改变，所以冒泡排序是稳定的排序算法。