桶排序

思想

将待排序列分到几个有序的桶里，每个桶里的数据再单独进行排序。桶内排完序之后，再把每个桶里的数据按照顺序依次取出，组成的序列就是有序的了。桶排序的关键是桶的划分，只要划分的合理，就可以接近线性时间复杂度。

为了更好的理解桶排序，可以结合下面的例子来理解排序过程：

eg: 对下面这组 50 元以内的订单进行排序:

22,5,11,41,45,26,29,10,7,8,30,27,42,43,40

桶排序可以将上述数据划分为 5 个桶，并将数据放到对应的桶中，如下图所示：

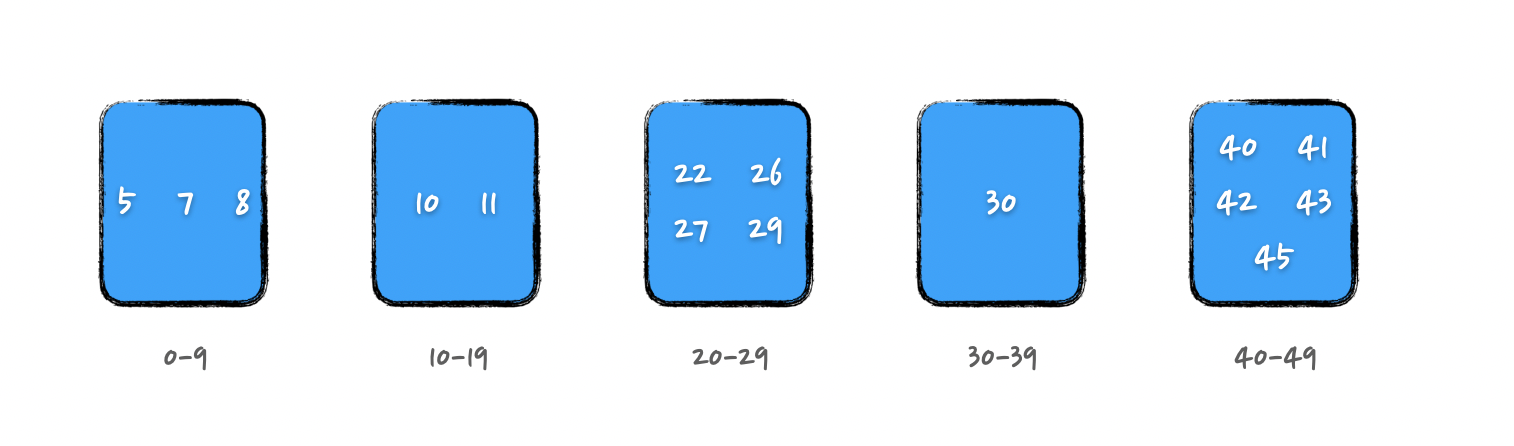
实现

// TODO

分析

时间复杂度

将 n 个待排数据划分到 m 个桶内，每个桶有 k=n/m 个元素。对每个桶内元素进行快速排序，时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk)，因为 k = n/m，所以桶排序的时间复杂度就是 O(n * log(n/m))。当桶的个数 m 接近数据个数 n 时，log(n/m) 就是一个非常小的常量，这个时候桶排序的时间复杂度接近 O(n)。

适用场景

桶排序比较适合的场景：数据存储在外部磁盘中，并且数据量比较大，内存有限，无法将数据全部加载到内存中。

例如，当想对 10GB 的订单数据做排序时，显然内存是处理不了的，此时我们可以采用桶排序以订单的价格来划分桶。假设订单的价格区间为 1 元到 10 万元，此时可以将金额划分到 100 个桶里，第一个桶为 1 到 1000 元，第二个桶为 1001 到 2000，...，依次类推。然后在再对每个桶的这些数据进行快速排序，再依次合并数据。

如果价格分布均匀的话，我们期望每个桶的数据量都是 100MB，一旦数据分布不均，我们需要对数据量较大的再进行划分，比如，订单金额在 1 元到 1000 元之间的比较多，我们就将这个区间继续划分为 10 个小区间，1 元到 100 元，101 元到 200 元，...，901 元到 1000 元。如果仍然还有不均匀，无法一次性读入内存，可以对其再化分。