递归与尾调用优化
对于你写的 97%的代码,多上几毫秒并不会有什么区别,特别是相对代码的可维护性来说。 - Knuth
对于大多数的应用而言,牺牲效率以获得更高的可维护性是值得考虑的。应该让代码更容易阅读和调试,即使它不是最快的。——《JavaScript 函数式编程指南》P178
递归
递归是把一个问题分解成两个或者多个一样的小问题,也是一种分治思想。
递归本质上是一种循环操作。纯粹的函数式编程语言没有循环操作命令,所有的循环都用递归实现,这就是为什么尾递归对这些语言极其重要。我们需要知道循环可以用递归代替,而一些递归不加以优化会容易爆栈,且效率相对比较低,但代码比较简洁和可读。
递归的问题
递归虽然有简洁的优点,但它同时也有显著的缺点:
- 时间消耗:每一次函数调用,都需要在内存栈中分配空间以保存参数、返回地址及临时变量,而且往栈里压入数据和弹出数据都需要时间。
- 重复计算:递归中有可能很多计算都是重复的,从而对性能带来很大的负面影响。递归的本质是把一个问题分解成两个或者多个小问题。如果多个小问题存在相互重叠的部分,就存在重复的计算。
- 调用栈溢出:这是递归最为致命的问题。前面提到需要为每一次函数调用在内存栈中分配空间,而每个进程的栈容量是有限的。当递归调用的层级太多时,就会超出栈的容量,从而导致调用栈溢出。
两个典型递归
阶乘
const factorial = n => (n === 1 ? 1 : n * factorial(n - 1)); // 最后一步不是只有递归
调用过程大致如下:
factorial(4)
4 * factorial(3)
4 * 3 * factorial(2)
4 * 3 * 2 * factorial(1)
4 * 3 * 2 * 1
4 * 3 * 2
4 * 6
return 24
不难发现这个版本的阶乘,函数调用栈会一直保留,时间和空间的消耗都不小,由于阶乘的结果比较大,很快就会超出 JS 的最大整数范围,所以还不至于在浏览器中爆栈,但调用时间相对比较慢。

factorial(100); // 0.123ms
factorial(100); // 0.126ms
斐波那契数列
斐波那契 (Fibonacci) 数列的第 n 项的定义如下:

function fibonacci(n) {
if (n <= 0) return 0;
if (n === 1) return 1;
return fibonacci(n - 1) + fibonacci(n - 2);
}
我们以求解 f(10) 为例来分析递归的求解过程。想求得 f(10),需要先求得 f(9) 和 f(8)。同样,想求得 f(9),需要先求得 f(8) 和 f(7)...我们何以用树形结构来表示这种依赖关系,如下图所示:
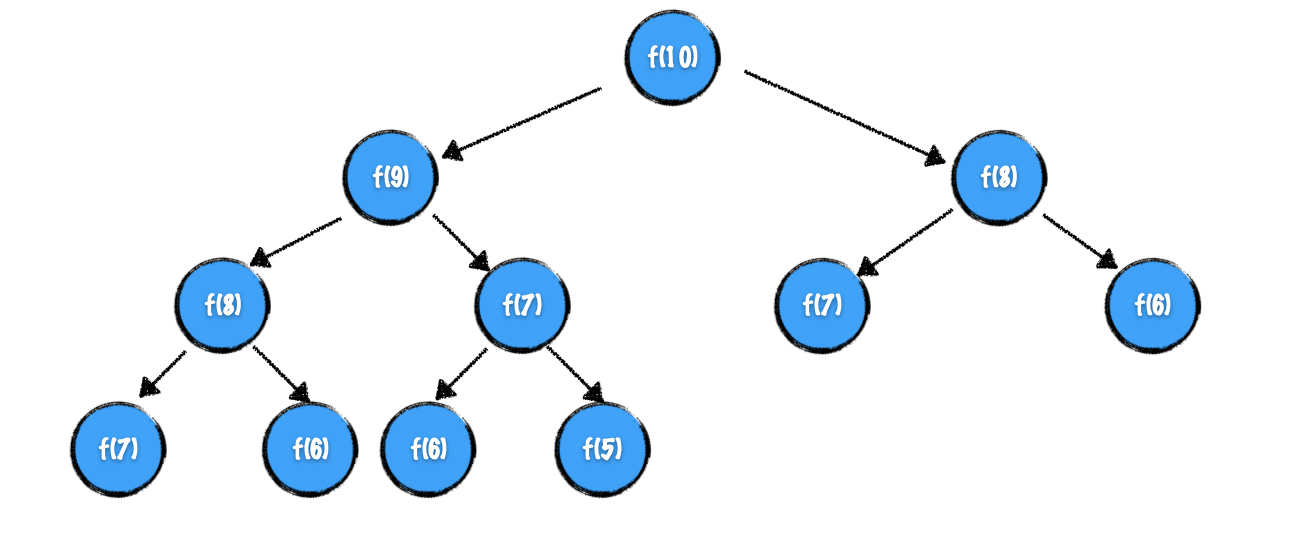
图:基于递归求斐波那契数列的第 10 项的调用过程
我们不难发现,在这棵树中有很多节点是重复的,而且重复的节点数会随着 n 的增大而急剧增加,这意味着计算量会随着 n 的增大而急剧增大。事实上,用递归方法计算的时间复杂度是以 n 的指数的方式递增的。比如输入 fibonacci(50) 返回结果是非常慢的,有可能会导致浏览器标签页挂掉。
其它递归常见的应用,比如在树的遍历等方面也是广泛应用。
通过记忆化优化递归
递归通过分解把问题化为更简单的自相似问题,继而利用记忆化优化上下文堆栈来优化递归调用的效率。
记忆化版阶乘
let factorial = memoize(factorial);
factorial(100); // 0.123ms
factorial(101); // 0.004ms
记忆化版斐波那契数列
let fibonacci = memoize(fibonacci);
fibonacci(100);
此时会发现别说是 fibonacci(50), 就连 fibonacci(100) 也是小菜一碟。
尾部调用优化
什么是 TCO
尾部调用优化(Tail Call Optimization)。尾递归带来递归循环的性能接近于 for 循环,没有额外创建堆栈帧。
简单地说,尾调用就是一个出现在另一个函数“结尾”处的函数调用。这个调用结束后就没有其余事情要做了(除了可能要返回结果值)。
function foo(x) {
return x;
}
function bar(y) {
return foo(y + 1); // 尾调用
}
function baz() {
return 1 + bar(40); // 非尾调用
}
baz(); // 42
foo(y+1) 是 bar(..) 中的尾调用,因为在 foo(..) 完成后,bar(..) 也完成了,并且只需要返回 foo(..) 调用的结果。然而,bar(40) 不是尾调用,因为在它完成后,它的结果需要加上 1 才能由 baz() 返回。
TCO 原理
TCO 是编译器级别的优化,我们知道调用一个新的函数需要额外的一块预留内存来管理调用栈,称为栈帧 。所以前面的代码一般 会同时需要为每个 baz()、bar(..) 和 foo(..) 保留一个栈帧。
然而,如果支持 TCO 的引擎能够意识到 foo(y+1) 调用位于尾部 ,这意味着 bar(..) 基本上已经完成了,那么在调用 foo(..) 时,它就不需要创建一个新的栈帧,而是可以重用已有的 bar(..) 的栈帧。这样不仅速度更快,也更节省内存。
在简单的代码片段中,这类优化算不了什么,但是在处理递归时,这就解决了大问题,特别是如果递归可能会导致成百上千个栈帧的时候。有了 TCO,引擎可以用同一个栈帧执行所有这类调用!
ES6 之所以要求引擎实现 TCO 而不是将其留给引擎自由决定,一个原因是缺乏 TCO 会导致一些 JavaScript 算法因为害怕调用栈限制而降低了通过递归实现的概率。
目前支持 TCO 只有 Safari 浏览器。
通过尾部调用优化递归
TCO 将函数的上下文状态作为参数传递给下一个函数调用,使得递归调用不依赖当前栈,那么可以抛弃当前的栈,从而达到扁平化栈释放内存的目的。
所以改成尾递归只需两步:
- 将当前乘法结果当作参数传入递归函数(有单参数改为多参数)
- 给结果参数传递一个默认值(类似于求和函数的默认值)
尾递归版阶乘
const factorial = (n, result = 1) =>
n === 1 ? result : factorial(n - 1, n * result); // 最后一步只有递归
factorial(4)
factorial(3, 4)
factorial(2, 12)
factorial(1, 24)
return 24